题目内容
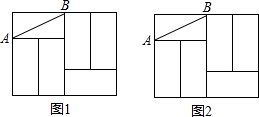
8. 如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD面积为4,则矩形AEFC的面积为4.
如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD面积为4,则矩形AEFC的面积为4.
分析 由于矩形ABCD的面积等于2个△ABC的面积,而△ABC的面积又等于矩形AEFC的一半,所以可得两个矩形的面积关系.
解答  解:过B作BE⊥AC于E,则BE=AE,
解:过B作BE⊥AC于E,则BE=AE,
∵S矩形ABCD=2S△ABC,
而S△ABC=$\frac{1}{2}$AC•BE=$\frac{1}{2}$AC•AE=$\frac{1}{2}$S矩形AEFC,
即S矩形ABCD=S矩形AEFC=4,
故答案为:4.
点评 本题主要考查了矩形的性质及面积的计算,能够熟练运用矩形的性质进行一些面积的计算问题.

练习册系列答案
相关题目
18. 某商场销售某种商品,原价560元,随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:
某商场销售某种商品,原价560元,随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:
(1)根据图象完成下表:
(2)售价为560元时,日销售量为750件.
(3)如果该商场要求日销售量为1110件,该商品应降价500元.
(4)设该商品的售价为x(x≤560)元,日销售量为y件,求y与x之间的关系式.
 某商场销售某种商品,原价560元,随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:
某商场销售某种商品,原价560元,随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:(1)根据图象完成下表:
| 降价/元 | 5 | 10 | 15 | 20 |
| 日销售量/件 | 780 | 810 | 840 | 870 |
(3)如果该商场要求日销售量为1110件,该商品应降价500元.
(4)设该商品的售价为x(x≤560)元,日销售量为y件,求y与x之间的关系式.
20.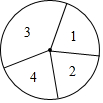 如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )
如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )
 如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )
如图是一个转盘,扇形1,2,3的圆心角分别是60°,70°,150°,任意转动转盘,指针指向扇形4的概率是( )| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
17.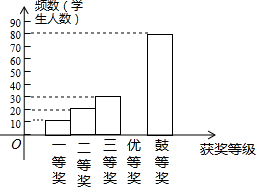 为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
请根据所给信息,解答下列问题:
(1)a=60,b=0.15,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)若我市初中生共有16000人,竞赛活动获奖率为40%,获三等奖以上的学生表示对“足球比较喜欢”,请你估计我市初中生对“足球比较喜欢”的有多少人?
 为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:| 获奖等次 | 频数 | 频率 |
| 一等奖 | 10 | 0.05 |
| 二等奖 | 20 | 0.10 |
| 三等奖 | 30 | b |
| 优胜奖 | a | 0.30 |
| 鼓励奖 | 80 | 0.40 |
(1)a=60,b=0.15,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)若我市初中生共有16000人,竞赛活动获奖率为40%,获三等奖以上的学生表示对“足球比较喜欢”,请你估计我市初中生对“足球比较喜欢”的有多少人?
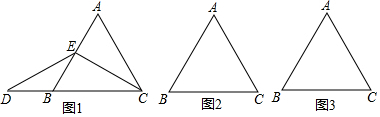
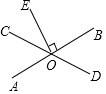 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=40°,求∠AOD的度数.
如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=40°,求∠AOD的度数. 平行四边形ABCD中,AE、BF分别平分∠DAB和∠ABC交CD于点E、F.AE、BF交于点G.
平行四边形ABCD中,AE、BF分别平分∠DAB和∠ABC交CD于点E、F.AE、BF交于点G.