题目内容
2．对称轴为直线x=1的抛物线y=ax2+bx+c与x轴的一个交点坐标为（3，0），则关于x的一元二次方程ax2+bx+c=0的根是x1=-1，x2=3．分析 根据抛物线与x轴的两个交点到对称轴的距离相等，设另一个交点为（x，0），可得$\frac{3+x}{2}$=1，解得x的值即可．
解答 解：设抛物线与x轴的另一个交点坐标为：（x，0），
∵抛物线与x轴的两个交点到对称轴的距离相等，
∴$\frac{3+x}{2}$=1，
解得：x=-1，
∴抛物线与x轴的另一个交点坐标为：（-1，0）．
所以关于x的一元二次方程ax2+bx+c=0的根是x1=-1，x2=3．
故答案是：x1=-1，x2=3．
点评 本题考查了求抛物线与x轴的交点问题，关键是掌握抛物线与x轴的两交点关于对称轴对称．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
13．等腰三角形的一个角是90°，则它的底角是（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
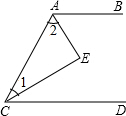如图，AE平分∠BAC，CE平分∠ACD，且∠1+∠2=90°．试说明CD∥AB．
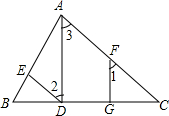已知AD⊥BC，FG⊥BC，垂足分别为D、G，且∠1=∠2，求证∠BDE=∠C．
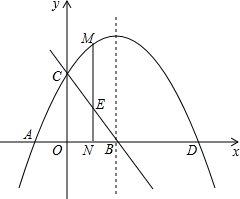如图，抛物线y=ax2+bx+4与x轴交于A（-2，0），D两点，与y轴交于点C，对称轴x=3交x轴交于点B．