题目内容
计算:x2+x+1=0,求x3-x2-x+7的值.
考点:因式分解的应用
专题:
分析:由x2+x+1=0得x2+x=-1,然后把它的值整体代入所求代数式,求值即可.
解答:解:由x2+x+1=0得x2+x=-1,
∴x3-x2-x+7
=x3+x2-2x2-x+7
=x(x2+x)-2x2-x+7
=-x-2x2-x+7
=-2(x2+x)+7
=2+7
=9.
∴x3-x2-x+7
=x3+x2-2x2-x+7
=x(x2+x)-2x2-x+7
=-x-2x2-x+7
=-2(x2+x)+7
=2+7
=9.
点评:本题考查因式分解的应用,代数式中的字母表示的数没有明确告知,而是隐含在题设中,首先应从题设中获取代数式x2+x的值,然后利用“整体代入法”求代数式的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
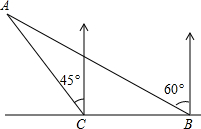 如图,海岛A四周30海里范围内是暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60°,航行20海里后到C处,见岛A在北偏西45°,货轮继续向西航行,有无触礁危险?
如图,海岛A四周30海里范围内是暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60°,航行20海里后到C处,见岛A在北偏西45°,货轮继续向西航行,有无触礁危险?