题目内容
思考后请填空:
(1)1+2+3+…+99+100= ;
(2)由此可得:1+2+3+…+n= .
(1)1+2+3+…+99+100=
(2)由此可得:1+2+3+…+n=
考点:有理数的加法
专题:
分析:(1)根据有理数的加法运算,可得答案;
(2)由(1)易得1+2+3+…+n=
(n2+n).
(2)由(1)易得1+2+3+…+n=
| 1 |
| 2 |
解答:解:(1)设S=1+2+3+4+5+…+99+100 ①,
S=100+99+…+3+2+1 ②,
①+②得
2S=(1+100)+(2+99)+…(2+99)+(100+1)
S=
=5050;
(2)设S=1+2+3+…+n①,
S=n+n-1+…+3+2+1②,
①+②得:2S=(1+n)+(2+n-1)+…(n-1+2)+(n+1)
S=
.
故答案为:5050;
.
S=100+99+…+3+2+1 ②,
①+②得
2S=(1+100)+(2+99)+…(2+99)+(100+1)
S=
| (1+100)×100 |
| 2 |
(2)设S=1+2+3+…+n①,
S=n+n-1+…+3+2+1②,
①+②得:2S=(1+n)+(2+n-1)+…(n-1+2)+(n+1)
S=
| n×(n+1) |
| 2 |
故答案为:5050;
| n(n+1) |
| 2 |
点评:本题考查了有理数的加法,利用了连续自然数的求和公式.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图,直线AB,CD相交于点O,OE分∠AOD成两个角,∠AOE:∠EOD=2:6,∠BOD-∠BOC=20°,求∠AOE的度数.
如图,直线AB,CD相交于点O,OE分∠AOD成两个角,∠AOE:∠EOD=2:6,∠BOD-∠BOC=20°,求∠AOE的度数. 用“>”或“<”号填空:有理数a,b,c在数轴上对应的点如图:
用“>”或“<”号填空:有理数a,b,c在数轴上对应的点如图: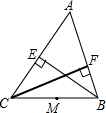 如图,BE、CF是△ABC的高,M为BC的中点.试说明点B、C、E、F在以点M为圆心的同一圆上.
如图,BE、CF是△ABC的高,M为BC的中点.试说明点B、C、E、F在以点M为圆心的同一圆上.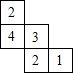 一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.