题目内容
15．若关于x的一元二次方程x2-3x+2m=0有两个不相等的实数根，则实数m的取值范围是（ ）| A． | m＞$\frac{9}{8}$ | B． | m≥$\frac{9}{8}$ | C． | m≤$\frac{9}{8}$ | D． | m＜$\frac{9}{8}$ |
分析 若一元二次方程有两不等根，则根的判别式△=b2-4ac＞0，建立关于m的不等式，求出m的取值范围．
解答 解：∵方程有两个不相等的实数根，a=1，b=-3，c=2m
∴△=b2-4ac=（-3）2-4×1×（2m）＞0，
解得m＜$\frac{9}{8}$，
故选D．
点评 考查了根的判别式，总结：一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．某商店需要购进一批电视机和洗衣机，根据市场调查，决定电视机进货量不少于洗衣机的进货量的一半．电视机与洗衣机的进价和售价如下表：
计划购进电视机和洗衣机共100台，商店最多可筹集资金161800元．
（不考虑除进价之外的其它费用）
（1）如果商店将购进的电视机与洗衣机销售完毕后获得利润为y元，购进电视机x台，求y与x的函数关系式（利润=售价-进价）
（2）请你帮助商店算一算有多少种进货方案？
（3）哪种进货方案待商店将购进的电视机与洗衣机销售完毕后获得利润最多？并求出最多利润．
| 类 别 | 电视机 | 洗衣机 |
| 进价（元/台） | 1800 | 1500 |
| 售价（元/台） | 2000 | 1600 |
（不考虑除进价之外的其它费用）
（1）如果商店将购进的电视机与洗衣机销售完毕后获得利润为y元，购进电视机x台，求y与x的函数关系式（利润=售价-进价）
（2）请你帮助商店算一算有多少种进货方案？
（3）哪种进货方案待商店将购进的电视机与洗衣机销售完毕后获得利润最多？并求出最多利润．
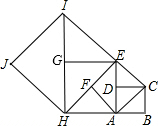如图，如果以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去…，已知正方形ABCD的面积S1为1，按上述方法所作的正方形的面积依次为S2，S3，…，Sn（n为正整数），那么第2015个正方形的面积S2015为22014．