题目内容
20．如果等腰三角形的两边长分别是方程x2-8x+12=0的两个根，则这个等腰三角形的周长是（ ）| A． | 10 | B． | 6或者2 | C． | 10或者14 | D． | 14 |
分析 求出方程的解，得出三角形的三边长，即可得出答案．
解答 解：解x2-8x+12=0地：x=6或2，
当三角形的三边为2，2，6时，不符合三角形三边关系定理，此时不能组成三角形；
当三角形的三边为2，6，6时，符合三角形三边关系定理，此时能组成三角形，三角形的周长为2+6+6=14，
故选D．
点评 本题考查了等腰三角形的性质，三角形的三边关系定理，解一元二次方程的应用，能求出方程的解是解此题的关键．
练习册系列答案
相关题目
10．下列三条线段中（单位长度都是cm），能组成三角形的是（ ）
| A． | 3，4，9 | B． | 50，60，12 | C． | 11，11，31 | D． | 20，30，50 |
8．下列轴对称图形中，对称轴条数最多的是（ ）
| A． | 线段 | B． | 等边三角形 | C． | 正方形 | D． | 圆 |
15．计算$\frac{1}{8}$×（-8）÷（-$\frac{1}{8}$）结果等于（ ）
| A． | 8 | B． | -8 | C． | $\frac{1}{8}$ | D． | 1 |
5．要判定两个直角三角形全等，下列说法正确的有（ ）
①有两条直角边对应相等；
②有两个锐角对应相等；
③有斜边和一条直角边对应相等；
④有一条直角边和一个锐角相等；
⑤有斜边和一个锐角对应相等；
⑥有两条边相等．
①有两条直角边对应相等；
②有两个锐角对应相等；
③有斜边和一条直角边对应相等；
④有一条直角边和一个锐角相等；
⑤有斜边和一个锐角对应相等；
⑥有两条边相等．
| A． | 6个 | B． | 5个 | C． | 4个 | D． | 3个 |
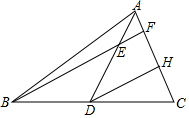如图，AD为△ABC的中线，AE=$\frac{1}{3}$AD，BE交AC于点F，DH∥BF，则$\frac{AF}{CH}$=$\frac{1}{2}$．
9．下列各式正确的是（ ）
| A． | $\sqrt{（-2）^{2}}$=-2 | B． | $\sqrt{4}$=±2 | C． | -22=4 | D． | -$\sqrt{9}$=-3 |