题目内容
 如图,在直角梯形ABCD中,AD∥BC,AD=1,BC=9,M为AB的中点,以CD为直径画圆P.
如图,在直角梯形ABCD中,AD∥BC,AD=1,BC=9,M为AB的中点,以CD为直径画圆P.(1)当点M在圆P外时,求CD的长的取值范围;
(2)当点M在圆P上时,求CD的长;
(3)当点M在圆P内时,求CD的长的取值范围.
考点:点与圆的位置关系
专题:
分析:(1)取CD的中点P,连接MP,则MP是梯形ABCD的中位线.求出MP长,由于点M在圆P外,则MP>PC,由此得出结论;
(2)根据点M在圆P上,则MP=PC,由此得出结论;
(3)根据点M在圆P内,则MP<PC,由此得出结论.
(2)根据点M在圆P上,则MP=PC,由此得出结论;
(3)根据点M在圆P内,则MP<PC,由此得出结论.
解答: 解:(1)取CD的中点P,连接MP,
解:(1)取CD的中点P,连接MP,
∵M为AB的中点,
∴MP是梯形ABCD的中位线.
∵AD=1,BC=9,
∴MP=
×(1+9)=5,
∵点M在圆P外,
∴MP>PC,即2MP>CD,
∴0<CD<10;
(2)∵点M在圆P上,
∴MP=PC,即2MP=CD,
∴CD=2×5=10;
(3)∵点M在圆P内,
∴MP<PC,即2MP<CD,
∴CD>10.
 解:(1)取CD的中点P,连接MP,
解:(1)取CD的中点P,连接MP,∵M为AB的中点,
∴MP是梯形ABCD的中位线.
∵AD=1,BC=9,
∴MP=
| 1 |
| 2 |
∵点M在圆P外,
∴MP>PC,即2MP>CD,
∴0<CD<10;
(2)∵点M在圆P上,
∴MP=PC,即2MP=CD,
∴CD=2×5=10;
(3)∵点M在圆P内,
∴MP<PC,即2MP<CD,
∴CD>10.
点评:本题考查的是点与圆的位置关系,熟知点与圆的3种位置关系是解答此题的关键.

练习册系列答案
相关题目
下列二次根式,属于最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
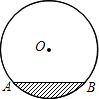 如图,是一个圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为32cm,水管半径为20cm,AB为⊙O的劣弧,求截面有水部分的最大深度.
如图,是一个圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为32cm,水管半径为20cm,AB为⊙O的劣弧,求截面有水部分的最大深度. 如图是某中学景点内的一个拱门,它是⊙O的一部分,已知拱门的地面宽度CD=2m,它的最大高度EM=3m,则构成拱门的⊙O的半径是
如图是某中学景点内的一个拱门,它是⊙O的一部分,已知拱门的地面宽度CD=2m,它的最大高度EM=3m,则构成拱门的⊙O的半径是