题目内容
 如图:D、E是三角形ABC的边BC上的两点,且BD=DE=AD=AE=EC,则∠BAC的大小等于
如图:D、E是三角形ABC的边BC上的两点,且BD=DE=AD=AE=EC,则∠BAC的大小等于考点:等边三角形的判定与性质,等腰三角形的性质
专题:
分析:由AD=AE=DE,可得△ADE是等边三角形,根据等边对等角可得∠ADE=∠AED=∠DAE=60°,由三角形外角的性质和等腰三角形的性质即可求得∠BAD与∠CAE的度数,继而求得答案.
解答:解:∵AD=AE=DE,
∴△ADE是等边三角形,
∴∠ADE=∠AED=∠DAE=60°,
∵AD=AB,AE=EC,
∴∠B=∠BAD,∠C=∠CAE,
∵∠ADE=∠B+∠BAD,∠AED=∠C+∠CAE,
∴∠BAD=∠CAE=30°,
∴∠BAC=∠BAD+∠DAE+∠CAE=120°.
故答案为:120°.
∴△ADE是等边三角形,
∴∠ADE=∠AED=∠DAE=60°,
∵AD=AB,AE=EC,
∴∠B=∠BAD,∠C=∠CAE,
∵∠ADE=∠B+∠BAD,∠AED=∠C+∠CAE,
∴∠BAD=∠CAE=30°,
∴∠BAC=∠BAD+∠DAE+∠CAE=120°.
故答案为:120°.
点评:此题考查了等腰三角形的性质以及等边三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
已知x=-3是方程k(x+4)-2k-x=5的解,则k的值是( )
| A、-2 | B、2 | C、3 | D、5 |
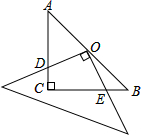 如图,在等腰Rt△ABC中,∠C=90°,点O是AB的中点,边AC的长为a,将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为点D,另一条直角边与BC相交,交点为点E,证明:等腰直角△ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值a.
如图,在等腰Rt△ABC中,∠C=90°,点O是AB的中点,边AC的长为a,将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为点D,另一条直角边与BC相交,交点为点E,证明:等腰直角△ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值a.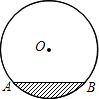 如图,是一个圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为32cm,水管半径为20cm,AB为⊙O的劣弧,求截面有水部分的最大深度.
如图,是一个圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为32cm,水管半径为20cm,AB为⊙O的劣弧,求截面有水部分的最大深度. 如图是某中学景点内的一个拱门,它是⊙O的一部分,已知拱门的地面宽度CD=2m,它的最大高度EM=3m,则构成拱门的⊙O的半径是
如图是某中学景点内的一个拱门,它是⊙O的一部分,已知拱门的地面宽度CD=2m,它的最大高度EM=3m,则构成拱门的⊙O的半径是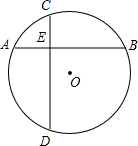 如图,已知在⊙O中,AB,CD两弦互相垂直于点E,AB被分成4cm和10cm两段.
如图,已知在⊙O中,AB,CD两弦互相垂直于点E,AB被分成4cm和10cm两段.