题目内容
1. 如图,平面直角坐标系中,△ABC为等边三角形,其中点A、B、C的坐标分别为(-3,-1)、(-3,-3)、(-3+$\sqrt{3}$,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
如图,平面直角坐标系中,△ABC为等边三角形,其中点A、B、C的坐标分别为(-3,-1)、(-3,-3)、(-3+$\sqrt{3}$,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.①直接写出点C1的坐标(3-$\sqrt{3}$,-2),点C2的坐标(3-$\sqrt{3}$,2);
②能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定的回答,并直接写出所旋转的度数;你若认为不能,请作出否定的回答(不必说明理由);
③设当△ABC的位置发生变化时,△A2B2C2、△A1B1C1、△ABC之间的对称关系始终保持不变,当△ABC向上平移多少个单位时,△A1B1C1与△A2B2C2完全重合?并直接写出此时点C的坐标?
分析 ①根据关于y轴对称的点的坐标特征写出C1点的坐标,然后根据关于x轴对称的点的坐标特征写出点C2的坐标;
②由于△ABC与△A1B1C1关于y轴对称,△A1B1C1与△A2B2C2关于x轴对称,则△ABC与△A2B2C2关于原点中心对称,于是根据中心对称的定义可判断旋转的度数;
③由于△A1B1C1与△A2B2C2关于x轴对称,而A1B1C1与△A2B2C2完全重合,则△A1B1C1是关于x轴的轴对称图形,所以△ABC也是关于x轴的轴对称图形,于是点C要平移到x轴,从而得到△ABC平移的距离.
解答 解:①点C1的坐标为(3-$\sqrt{3}$,-2),点C2的坐标为(3-$\sqrt{3}$,2);
故答案为(3-$\sqrt{3}$,-2),(3-$\sqrt{3}$,2);
②将△ABC绕点O旋转180°可得到△A2B2C2,即旋转的度数为180°;
③当△ABC向上平移2个单位时,△A1B1C1与△A2B2C2完全重合,此时点C的坐标为(-3+$\sqrt{3}$,0).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
相关题目
16.下列关于一元二次方程x2-3x=-1的各项系数说法正确的是( )
| A. | 二次项系数为0 | B. | 一次项系数为3 | C. | 常数项为-1 | D. | 以上说法都不对 |
13.如图是一个立体图的主视图左视图和俯视图(图中单位为厘米),则立体图形的体积为多少?( )
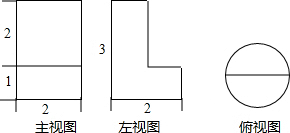

| A. | π | B. | 2π | C. | 3π | D. | 4π |
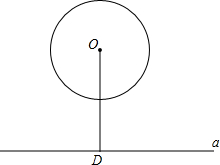 如图,⊙O的半径为3cm,OD垂直于直线a,垂足为D,OD=4cm,问直线a向上平移几厘米时,直线a与⊙O有一个公共点?
如图,⊙O的半径为3cm,OD垂直于直线a,垂足为D,OD=4cm,问直线a向上平移几厘米时,直线a与⊙O有一个公共点? 如图,根据展开图画出物体的三视图,并求物体的体积和表面积.
如图,根据展开图画出物体的三视图,并求物体的体积和表面积.