题目内容
8.计算:(1)2x2-3x-2=0;
(2)|$\sqrt{3}-3$|+(π-3)0+tan60°.
分析 (1)利用因式分解法解方程;
(2)根据零指数幂的意义和特殊角的三角函数值得到原式=3-$\sqrt{3}$+1+$\sqrt{3}$,然后合并即可.
解答 解:(1)(2x+1)(x-2)=0,
2x+1=0或x-2=0,
所以x1=-$\frac{1}{2}$,x2=2;
(2)原式=3-$\sqrt{3}$+1+$\sqrt{3}$
=4.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了实数的运算.

练习册系列答案
相关题目
18.下列式子正确的是( )
| A. | -$\frac{4}{5}$>-$\frac{5}{4}$ | B. | -$\frac{3}{4}$<-$\frac{4}{5}$ | C. | 0<-|-100| | D. | -(-2$\frac{1}{2}$)>|-2.5| |
13.下列各式中,分式的个数为( )
$\frac{x-y}{3}$,$\frac{a}{2x-1}$,$\frac{x}{π+1}$,-$\frac{3a}{b}$,$\frac{1}{2x+y}$,$\frac{1}{2}x+y$.
$\frac{x-y}{3}$,$\frac{a}{2x-1}$,$\frac{x}{π+1}$,-$\frac{3a}{b}$,$\frac{1}{2x+y}$,$\frac{1}{2}x+y$.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20. 有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是( )
有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是( )
 有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是( )
有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是( )| A. | a>b | B. | a+b>0 | C. | ab<0 | D. | |a|<|b| |
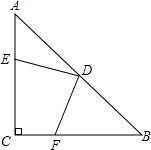 已知:如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF. 实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,
实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,