题目内容
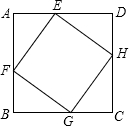 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为 ,则|a-b|等于
,则|a-b|等于
- A.

- B.

- C.

- D.

D
分析:易证图形中的四个小三角形全等,求出小三角形的面积,可得ab的值,根据四边形EFGH的面积,可求出a2+b2的值,得出(a-b)2的值,即可得出答案.
解答:∵正方形EFGH的面积为 ,
,
∴EF2= ,
,
在Rt△AEF中,AE2+AF2=EF2,即a2+b2= ,
,
由题意得:∠AFE=∠BGF(都是∠BFG的余角),
在△AEF和△BFG中,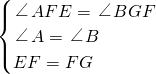 ,
,
∴△AEF≌△BFG(AAS),
同理可得:△AEF≌△BFG≌△CGH≌△DHE,
∴S△AEF= (S正方形ABCD-S正方形EFGH)=
(S正方形ABCD-S正方形EFGH)= ,
,
∴ab= ,
,
∴(a-b)2=a2+b2-2ab= ,
,
∴|a-b|= .
.
故选D.
点评:本题考查了正方形的性质,解答本题的关键是将求解的式子转换为求(a-b)2的值,也可以按部就班解a、b再求解,不过稍显麻烦一些.
分析:易证图形中的四个小三角形全等,求出小三角形的面积,可得ab的值,根据四边形EFGH的面积,可求出a2+b2的值,得出(a-b)2的值,即可得出答案.
解答:∵正方形EFGH的面积为
 ,
,∴EF2=
 ,
,在Rt△AEF中,AE2+AF2=EF2,即a2+b2=
 ,
,由题意得:∠AFE=∠BGF(都是∠BFG的余角),
在△AEF和△BFG中,
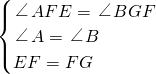 ,
,∴△AEF≌△BFG(AAS),
同理可得:△AEF≌△BFG≌△CGH≌△DHE,
∴S△AEF=
 (S正方形ABCD-S正方形EFGH)=
(S正方形ABCD-S正方形EFGH)= ,
,∴ab=
 ,
,∴(a-b)2=a2+b2-2ab=
 ,
,∴|a-b|=
 .
.故选D.
点评:本题考查了正方形的性质,解答本题的关键是将求解的式子转换为求(a-b)2的值,也可以按部就班解a、b再求解,不过稍显麻烦一些.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 19、如图,ABCD是边长为6的正方形,请你建立一个适当的平面直角坐标系,并分别写出A、B、C、D的坐标.
19、如图,ABCD是边长为6的正方形,请你建立一个适当的平面直角坐标系,并分别写出A、B、C、D的坐标.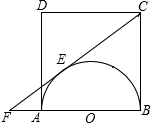 如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长.
如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长. 如图,ABCD是边长为9的正方形,E是BC上的一点,BE=
如图,ABCD是边长为9的正方形,E是BC上的一点,BE=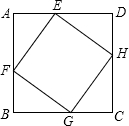 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为