题目内容
 如图,ABCD是边长为9的正方形,E是BC上的一点,BE=
如图,ABCD是边长为9的正方形,E是BC上的一点,BE=| 1 | 2 |
分析:由BE=
EC,可求得BE=3,利用勾股定理求得AE,由于MN为折痕,可得MN⊥AE,AK=
AE,利用三角形相似,求出AN的长即可求得本题答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:∵BE=
解:∵BE=
EC,BC=AB=9,
∴BE=
BC=
×9=3,
Rt△ABE中,AE=
=
=3
,
∵MN为折痕,
∴MN⊥AE,AK=
AE=
,
∵△ANK∽△AEB,
∴
=
,
即
=
,
解得AN=5,
∴S△ANE=
AN×BE=
×5×3=
.
故答案为:
.
 解:∵BE=
解:∵BE=| 1 |
| 2 |
∴BE=
| 1 |
| 3 |
| 1 |
| 3 |
Rt△ABE中,AE=
| AB2+BE2 |
| 92+32 |
| 10 |
∵MN为折痕,
∴MN⊥AE,AK=
| 1 |
| 2 |
3
| ||
| 2 |
∵△ANK∽△AEB,
∴
| AN |
| AE |
| AK |
| AB |
即
| AN | ||
3
|
| ||||
| 9 |
解得AN=5,
∴S△ANE=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
故答案为:
| 15 |
| 2 |
点评:本题考查了翻折问题及正方形的性质;通过折叠,找着的量,利用三角形相似求得AN的长是正确解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 19、如图,ABCD是边长为6的正方形,请你建立一个适当的平面直角坐标系,并分别写出A、B、C、D的坐标.
19、如图,ABCD是边长为6的正方形,请你建立一个适当的平面直角坐标系,并分别写出A、B、C、D的坐标.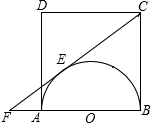 如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长.
如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长.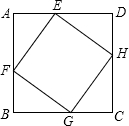 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若正方形EFGH的面积为