题目内容
8.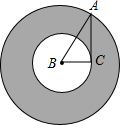 如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{2}$,将其绕B点顺时针旋转一周,则分别以BA、BC为半径的圆形成一个圆环,则该圆环的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AC=$\sqrt{2}$,将其绕B点顺时针旋转一周,则分别以BA、BC为半径的圆形成一个圆环,则该圆环的面积为( )| A. | $\sqrt{2}π$ | B. | 2π | C. | 4π | D. | 6π |
分析 根据勾股定理,得两圆的半径的平方差即是AC的平方.再根据圆环的面积计算方法:大圆的面积减去小圆的面积,即可求出答案.
解答 解:圆环的面积为πAB2-πBC2,
=π(AB2-BC2),
=πAC2,
=($\sqrt{2}$)2π,
=2π.
故选B.
点评 此题考查了勾股定理的知识,注意根据勾股定理把两个圆的半径的平方差进行转化成已知的数据即可计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
 如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )| A. | 的 | B. | 中 | C. | 国 | D. | 梦 |
16.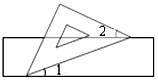 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )
 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )| A. | 20o | B. | 25o | C. | 30o | D. | 15o |
17.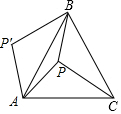 P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
 P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )| A. | 4$\sqrt{3}$+6 | B. | 12$\sqrt{3}$+6 | C. | 60 | D. | 42 |
 (1)用斜二测画法补全长方体ABCD-A1B1C1D1 (不必写画法);
(1)用斜二测画法补全长方体ABCD-A1B1C1D1 (不必写画法);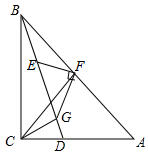 如图,在Rt△ABC中,∠ACB=90°,AC=BC,D是AC上一点,CG⊥BD于点G,点E在BD上,且BE=CG,点F是AB的中点,连接FE,FG,FC
如图,在Rt△ABC中,∠ACB=90°,AC=BC,D是AC上一点,CG⊥BD于点G,点E在BD上,且BE=CG,点F是AB的中点,连接FE,FG,FC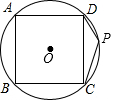 如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠DPC的度数是135度.
如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠DPC的度数是135度.