题目内容
17．
若将等腰直角三角形AOB按如图所示放置，斜边OB与x轴重合，OB=4，则点A关于原点对称的点的坐标为（-2，-2）．
分析 过点A作AD⊥OB于点D，根据等腰直角三角形的性质求出OD及AD的长，故可得出A点坐标，再由关于原点对称的点的坐标特点即可得出结论．
解答 
解：过点A作AD⊥OB于点D，
∵△AOB是等腰直角三角形，OB=4，
∴OD=AD=2，
∴A（2，2），
∴点A关于原点对称的点的坐标为（-2，-2）．
故答案为（-2，-2）．
点评 本题考查的是关于原点对称的点的坐标特点，熟知等腰直角三角形的性质是解答此题的关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
8．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD=（ ）
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD=（ ）| A． | 128° | B． | 100° | C． | 64° | D． | 32° |
如图，已知∠1=∠2，∠3=∠4，试说明AB∥CD．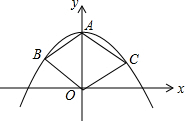
如图，在平面直角坐标系中，二次函数y=ax2+c（a＜0）的图象过菱形ABOC的三个顶点A、B、C，∠BAC=120°，则ac的值是-$\frac{2}{3}$．