题目内容
1. 如图,O为△ABC中∠ABC与∠ACB的平分线的交点,分别过点B、C作PB⊥BO,PC⊥CO,若∠A=70°,求出∠P的度数.
如图,O为△ABC中∠ABC与∠ACB的平分线的交点,分别过点B、C作PB⊥BO,PC⊥CO,若∠A=70°,求出∠P的度数.
分析 先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的定义求出∠OBC+∠OCB的度数,根据三角形内角和定理求出∠O的度数,再由四边形的内角和等于360°即可得出结论.
解答 解:∵△ABC中∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∵O为△ABC中∠ABC与∠ACB的平分线的交点,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×110°=55°,
∴∠O=180°-55°=125°,
∵PB⊥BO,PC⊥CO,
∴∠OBP=∠OCP=90°,
∴∠P=360°--∠OBP-∠OCP-∠O
=360°-90°-90°-125°
=55°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和定理、角平分线的定义及垂直的定义是解答此题的关键.

练习册系列答案
相关题目
9.抛物线y=2x2+1向下平移2个单位,再向左平移3个单位,得到的新抛物线的解析式为( )
| A. | y=2(x+3)2+3 | B. | y=2(x-3)2+3 | C. | y=2(x+3)2-1 | D. | y=2(x-3)2-1 |
6.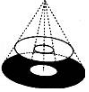 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )| A. | 0.324π m2 | B. | 0.288π m2 | C. | 1.08π m2 | D. | 0.72π m2 |
13.下列说法正确的是( )
| A. | b的指数是0 | B. | b没有系数 | C. | a是单项式 | D. | -3是一次单项式 |
11.一个正多边形的内角和是540°,这个多边形每个内角的度数是( )
| A. | 108° | B. | 118° | C. | 98° | D. | 72° |
 如图所示的几何体是由五个完全相同的正方体组成的,它的主视图是( )
如图所示的几何体是由五个完全相同的正方体组成的,它的主视图是( )



 如图,小山岗的斜坡AC的坡度是tanα=$\frac{3}{4}$,在与山脚C距离200m的D处,测得山顶A的仰角为26.6°,则小山岗的高AB=300米(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
如图,小山岗的斜坡AC的坡度是tanα=$\frac{3}{4}$,在与山脚C距离200m的D处,测得山顶A的仰角为26.6°,则小山岗的高AB=300米(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).