题目内容
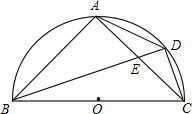 如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=
如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=| 5 |
(1)求直径BC的长;
(2)求弦AB的长.
考点:圆周角定理,勾股定理,相似三角形的判定与性质
专题:
分析:(1)首先可得∠BDC=90°,求出DE,再由△ADE∽△BCE,可得BC;
(2)由△ABE∽△DCE,可得
=
=
,设AE=x,在△ABC中利用勾股定理解出x,继而可得AB的长.
(2)由△ABE∽△DCE,可得
| AE |
| AB |
| DE |
| DC |
| 1 |
| 2 |
解答:解:(1)∵BC是半圆O的直径,
∴∠BDC=90°,
由CE=
,CD=2,得DE=1,
∵△ADE∽△BCE,
∴
=
,
∴BC=2
.
(2)∵△ABE∽△DCE,
∴
=
=
,
设AE=x,
∵AB2+AC2=BC2,
∴(x+
)2+(2x)2=(2
)2,
解得:x=
,
∵x>0,
∴x=
,
∴AB=2x=
.
∴∠BDC=90°,
由CE=
| 5 |
∵△ADE∽△BCE,
∴
| AD |
| BC |
| DE |
| CE |
∴BC=2
| 5 |
(2)∵△ABE∽△DCE,
∴
| AE |
| AB |
| DE |
| DC |
| 1 |
| 2 |
设AE=x,
∵AB2+AC2=BC2,
∴(x+
| 5 |
| 5 |
解得:x=
-2
| ||||
| 10 |
∵x>0,
∴x=
| 3 |
| 5 |
| 5 |
∴AB=2x=
| 6 |
| 5 |
| 5 |
点评:本题考查了圆周角定理,涉及了勾股定理及相似三角形的判定与性质,解答本题的关键是掌握相似三角形的对应边成比例.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若二次函数y=ax2的图象经过点P(2,8),则该图象必经过点( )
| A、(2,-8) |
| B、(-2,8) |
| C、(8,-2) |
| D、(-8,2) |
 在一个正方体的六个外表面上都写有汉字,其平面展开图如图所示,那么该正方体中和“美”字相对的汉字是( )
在一个正方体的六个外表面上都写有汉字,其平面展开图如图所示,那么该正方体中和“美”字相对的汉字是( )| A、好 | B、宁 | C、设 | D、隧 |
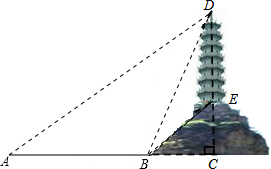 兴趣小组在一次数学实践活动中,为了测量如图所示的小山顶的塔高,进行了如下的操作,首先在A处测得塔尖D的仰角为30°,然后沿AC方向前进72米到达山脚B处,此时测得塔尖D的仰角为60°,塔底E的仰角为45°,求塔高.(结果保留根号)
兴趣小组在一次数学实践活动中,为了测量如图所示的小山顶的塔高,进行了如下的操作,首先在A处测得塔尖D的仰角为30°,然后沿AC方向前进72米到达山脚B处,此时测得塔尖D的仰角为60°,塔底E的仰角为45°,求塔高.(结果保留根号) 请画出如图中空心圆柱的三视图.
请画出如图中空心圆柱的三视图.