题目内容
已知⊙O是△ABC的外接圆,OD⊥BC于D,且∠BOD=32°,则∠BAC= °.
考点:圆周角定理,垂径定理
专题:
分析:分类讨论:当点O在△ABC的外部;当点O在△ABC的内部.先根据垂径定理得到BD=CD,利用等腰三角形的性质即可得到∠COD=∠BOD=32°,然后求出∠BAC所对的圆心角的度数,再根据圆周角定理得到∠BAC的度数.
解答: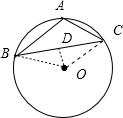 解:当点O在△ABC的外部,如图,连OC,
解:当点O在△ABC的外部,如图,连OC,
∵OD⊥BC,
∴BD=CD,
∴∠COD=∠BOD=32°,
∴优弧BC所对的圆心角∠BOC=360°-32°-32°=296°,
∴∠BAC=
×296°=148°;
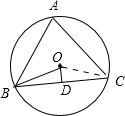 当点O在△ABC的内部,如图,连OC,
当点O在△ABC的内部,如图,连OC,
同理可得∠COD=∠BOD=32°,
∴∠BOC=64°,
∴∠BAC=
∠BOC=32°.
故答案为:32或148.
 解:当点O在△ABC的外部,如图,连OC,
解:当点O在△ABC的外部,如图,连OC,∵OD⊥BC,
∴BD=CD,
∴∠COD=∠BOD=32°,
∴优弧BC所对的圆心角∠BOC=360°-32°-32°=296°,
∴∠BAC=
| 1 |
| 2 |
 当点O在△ABC的内部,如图,连OC,
当点O在△ABC的内部,如图,连OC,同理可得∠COD=∠BOD=32°,
∴∠BOC=64°,
∴∠BAC=
| 1 |
| 2 |
故答案为:32或148.
点评:本题考查了圆周角定理:在同圆和等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.也考查了垂径定理以及分类讨论思想的运用.

练习册系列答案
相关题目
关于方程式5(x-2)2=8的两根,下列判断正确的是( )
| A、一根小于1,另一根大于3 |
| B、一根小于-2,另一根大于2 |
| C、两根都小于0 |
| D、两根都大于2 |
一个两位数,十位上的数字比个位上的数字小2,设十位上的数字为x,则这个两位数可表示为( )
| A、x+x-2 |
| B、x+x+2 |
| C、10x+x-2 |
| D、10x+x+2 |
在平面直角坐标系中,点P(-1,5)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
立方根为3的数是( )
| A、9 | B、27 | C、-27 | D、6 |
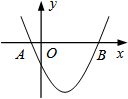 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(5,0),下列判断:
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(5,0),下列判断: