题目内容
19.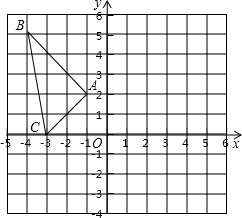 如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(-1,2),B(-4,5),C(-3,0).将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,其中点A′,B′,分别为点A,B,C的对应点.
如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(-1,2),B(-4,5),C(-3,0).将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,其中点A′,B′,分别为点A,B,C的对应点.(1)请在所给坐标系中画出△A′B′C′,并直接写出点C′的坐标;
(2)若AB边上一点P经过上述平移后的对应点为P′(x,y),用含x,y的式子表示点P的坐标;(直接写出结果即可)
(3)求△A′B′C′的面积.
分析 (1)根据网格结构找出点A′、B′、C′的位置,然后顺次连接即可,再根据平面直角坐标系写出点C′的坐标;
(2)根据向右平移横坐标加,向下平移纵坐标减解答;
(3)利用△A′B′C′所在的矩形的面积减去四周三个直角三角形的面积,列式计算即可得解.
解答 解:(1)△A′B′C′如图所示;点C′的坐标为(2,-2);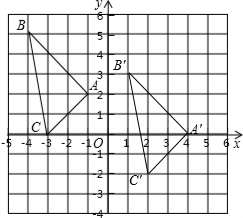
(2)点P的坐标为(x-5,y+2);
(3)△A′B′C′的面积=3×5-$\frac{1}{2}$×1×5-$\frac{1}{2}$×2×2-$\frac{1}{2}$×3×3=15-$\frac{5}{2}$-2-$\frac{9}{2}$=15-9=6.
点评 本题考查了利用平移变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
9.温家宝总理在2012年3月的政府工作报告中指出,2012年,再解决60 000 000农村人口的安全饮水问题.将60 000 000用科学记数法表示应为( )
| A. | 6×106 | B. | 6×107 | C. | 6×108 | D. | 60×106 |
14.去年我市有56940名初中毕业生参加升学考试,为了了解这56940名考生的数学成绩.从中抽取2000名考生的数学成绩进行统计分析.在这个问题中样本是( )
| A. | 56940名考生 | B. | 所抽取的2000名考生的数学成绩 | ||
| C. | 56940名考生的数学成绩 | D. | 所抽取的2000名考生 |
11.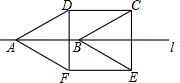 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )| A. | 2cm2 | B. | 3cm2 | C. | 4cm2 | D. | 6cm2 |
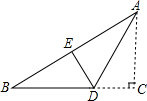 如图,折叠直角三角形纸片的直角,使点C落在AB边上的点E处,已知BC=12,∠B=30°,则DE=4.
如图,折叠直角三角形纸片的直角,使点C落在AB边上的点E处,已知BC=12,∠B=30°,则DE=4.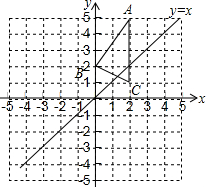 △ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1).
△ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1). 如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=126°.
如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=126°.