题目内容
如图,OA=OC,OB=OD且OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC; 其中正确的结论是( )
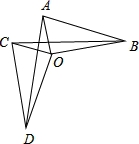
A.①② B.①②③ C.①③ D.②③
B【考点】全等三角形的判定与性质.
【分析】先由条件OA=OC,OB=OD且OA⊥OB,OC⊥OD就可以得出△COD≌△AOB,就有DD=BO,CD=AB,进而可以得出△AOD≌△COB就有∠ADO=∠CBO,从而得出结论.
【解答】解:∵OA⊥OB,OC⊥OD,
∴∠AOB=∠COD=90°.
∴∠AOB+∠AOC=∠COD+∠AOC,
即∠COB=∠AOD.
在△AOB和△COD中,
 ,
,
∴△AOB≌△COD(SAS),
∴AB=CD,∠ABO=∠CDO.
在△AOD和△COB中
 ,
,
∴△AOD≌△COB(SAS)
∴∠CBO=∠ADO,
∴∠ABO﹣∠CBO=∠CDO﹣∠ADO,
即∠ABC=∠CDA.
综上所述,①②③都是正确的.
故选B.
【点评】本题考查了全等三角形的判定与性质的运用,等式的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图, 一个4×2的矩形可以用3种不同的方式分割成2或5或8
个小正方形.
 |
⑴ 一个3×2的矩形用不同的方式分割后, 小正方形的个数可以是 ;
一个5×2的矩形用不同的方式分割后, 小正方形的个数可以是 ;
⑵ 一个n×2的矩形用不同的方式分割后,小正方形的个数最少是____________________.
(直接填写结果).
 有意义,则
有意义,则 的取值范围是 .
的取值范围是 . N,NH交∠CDG的平
N,NH交∠CDG的平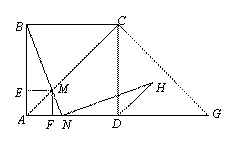

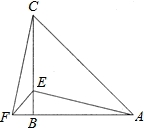
 的值.
的值.
 ,当函数值y随x的增大而减小时,x的取值范围是( )
,当函数值y随x的增大而减小时,x的取值范围是( )