题目内容
2.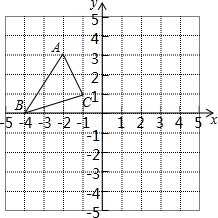 如图,已知△ABC的三个顶点在格点上.
如图,已知△ABC的三个顶点在格点上.(1)△ABC的三边中长度为$\sqrt{5}$的边为AC;
(2)作出与△ABC关于x轴对称的△A1B1C1;
(3)写出下列点的坐标:A1(-2,-3)、B1(-4,0) C1(-1,-1).
分析 (1)利用勾股定理可的AC=$\sqrt{{2}^{2}+{1}^{2}}$;
(2)首先确定A、B、C三点的对称点,然后再顺次连接即可;
(3)根据坐标系写出个点坐标即可.
解答  解:(1))△ABC的三边中长度为$\sqrt{5}$的边为:AC.
解:(1))△ABC的三边中长度为$\sqrt{5}$的边为:AC.
(2)如图所示:
(3)A1(-2,-3 )、B1(-4,0 )、C1(-1,-1 ).
点评 此题主要考查了作图--轴对称变换,以及勾股定理的应用,关键是掌握画一个图形的轴对称图形时,要先确定一些特殊的对称点.

练习册系列答案
相关题目
10.一个多边形的内角和为720°,那么这个多边形的对角线条有( )
| A. | 6条 | B. | 7条 | C. | 8条 | D. | 9条 |
7.多项式x3y2-5x2y+6xy-3的次数是( )
| A. | 2 | B. | 3 | C. | 5 | D. | 10 |
12.已知代数式a2+4a-2的值为3,则代数式a-1的值为( )
| A. | -5或1 | B. | -6或0 | C. | 0 | D. | -6 |
 如图,在△ABC中,∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D,则AD的长为12.
如图,在△ABC中,∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D,则AD的长为12. 如图,已知D为AC边上的中点,AE∥BC,EF过点D交BC于F,交AE于E,AE=a,BF=b,求BC的长.
如图,已知D为AC边上的中点,AE∥BC,EF过点D交BC于F,交AE于E,AE=a,BF=b,求BC的长.