题目内容
已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE.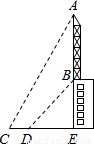
【答案】分析:根据从点D处测得天线下端B的仰角为45°,得出DE=BE,再利用tanC= ,得出BE的长即可.
,得出BE的长即可.
解答:解:∵从点D处测得天线下端B的仰角为45°,
∴DE=BE.
设BE=x米,则
∴AE=(x+25)米,CE=(x+6)米,
∵在点C处测得天线顶端A的仰角为60°,
∴tanC= ,
,
∴ =
= ,
,
∴x= ×(7+19
×(7+19 ),
),
即楼高BE= ×(7+19
×(7+19 )米.
)米.
点评:此题主要考查了仰角的定义及其解直角三角形的应用,解题时首先正确理解仰角的定义,然后利用三角函数和已知条件构造方程解决问题.
 ,得出BE的长即可.
,得出BE的长即可.解答:解:∵从点D处测得天线下端B的仰角为45°,
∴DE=BE.
设BE=x米,则
∴AE=(x+25)米,CE=(x+6)米,
∵在点C处测得天线顶端A的仰角为60°,
∴tanC=
 ,
,∴
 =
= ,
,∴x=
 ×(7+19
×(7+19 ),
),即楼高BE=
 ×(7+19
×(7+19 )米.
)米.点评:此题主要考查了仰角的定义及其解直角三角形的应用,解题时首先正确理解仰角的定义,然后利用三角函数和已知条件构造方程解决问题.

练习册系列答案
相关题目
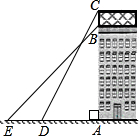 已知:如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在一条直线上的三点A(A为楼底)、D、E,她在D处测得广告牌顶端C的仰角为60°,在E两处测得商场大楼楼顶B 的仰角为45°,DE=5米.已知,广告牌的高度BC=2.35米,求这座商场大楼的高度AB(
已知:如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在一条直线上的三点A(A为楼底)、D、E,她在D处测得广告牌顶端C的仰角为60°,在E两处测得商场大楼楼顶B 的仰角为45°,DE=5米.已知,广告牌的高度BC=2.35米,求这座商场大楼的高度AB(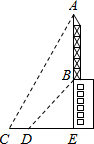 (2005•闸北区二模)已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE.
(2005•闸北区二模)已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE. 已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE.
已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE.