Question

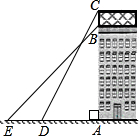已知：如图，一座商场大楼的顶部竖直立有一个矩形广告牌，小红同学在地面上选择了在一条直线上的三点A（A为楼底）、D、E，她在D处测得广告牌顶端C的仰角为60°，在E两处测得商场大楼楼顶B 的仰角为45°，DE=5米．已知，广告牌的高度BC=2.35米，求这座商场大楼的高度AB（

3

取1.73，

2

取1.41，小红的身高不计，结果保留整数）．

Answer 1

分析：由于在E出的仰角是45°，所以可得AE=AB，可设其值为x，再结合D出的仰角60°以及题中的条件，进而求解直角三角形即可．

解答：解：设AB为x米．
依题意，在Rt△ABE中，∠BEA=45°，
∴AE=AB=x．
∴AD=AE-DE=x-5，AC=BC+AB=2.35+x．
在Rt△ADC中，∠CDA=60°，
∴AC=AD•tan∠CDA=

3

AD．
∴x+2.35=

3

（x-5）．
∴（

3

-1）x=2.35+5

3

．
解得x=

5 3 +2.35

3 -1

．
∴x≈15．
答：商场大楼的高度AB约为15米．

点评：本题主要考查了生活中仰角俯角的问题，其中解题关键还是解直角三角形的问题，应熟练掌握．