题目内容
14.解方程:(1)$\frac{1}{x-1}$=$\frac{1}{{x}^{2}-1}$;
(2)$\frac{1}{x-2}$+3=$\frac{x-1}{x-2}$;
(3)$\frac{2-x}{3+x}$=$\frac{1}{2}$+$\frac{1}{x+3}$.
分析 (1)先把分式方程变成整式方程,求出方程的解,最后进行检验即可;
(2)先把分式方程变成整式方程,求出方程的解,最后进行检验即可;
(3)先把分式方程变成整式方程,求出方程的解,最后进行检验即可.
解答 解:(1)方程两边都乘以(x+1)(x-1)得:x+1=1,
解得:x=0,
检验:把x=0代入(x+1)(x-1)≠0,
所以x=0是原方程的解,
所以原方程的解为x=0;
(2)方程两边都乘以x-2得:1+3(x-2)=x-1,
解得:x=2,
检验:把x=2代入x-2=0,
所以x=2不是原方程的解,
所以原方程无解;
(3)方程两边都乘以2(x+3)得:2(2-x)=3+x+2,
解得:x=-$\frac{1}{3}$,
检验:把x=-$\frac{1}{3}$代入2(x+3)≠0,
所以x=-$\frac{1}{3}$是原方程的解,
所以原方程的解为x=-$\frac{1}{3}$.
点评 本题考查了解分式方程的应用,能把分式方程变成整式方程是解此题的关键,注意:解分式方程一定要进行检验.

练习册系列答案
相关题目
3.方程2x2-8=0的根是( )
| A. | x=2 | B. | x=-2 | C. | x1=2,x2=-2 | D. | x1=4,x2=-4 |

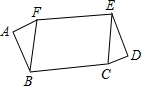 如图,已知BC=EF,BC∥EF,∠A=∠D,∠ABF=∠DEC,求证:AF=DC.
如图,已知BC=EF,BC∥EF,∠A=∠D,∠ABF=∠DEC,求证:AF=DC. 已知:如图,AB=AC,点D、E分别在AB、AC上,且AD=AE,求证:△ABE≌△ACD.
已知:如图,AB=AC,点D、E分别在AB、AC上,且AD=AE,求证:△ABE≌△ACD.