题目内容
10. 某校数学课外兴趣小组活动时,老师提出如下问题:
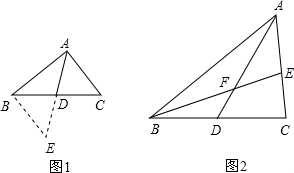
某校数学课外兴趣小组活动时,老师提出如下问题:【探究】如图1,△ABC中,若AB=8,AC=6,点D是BC的中点,试探究BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,请补充完整证明“△ADC≌△EDB”的推理过程.
(1)求证:△ADC≌△EDB
证明:∵延长AD到点E,使DE=AD
在△ADC和△EDB中AD=ED(已作)∠ADC=∠EDB(对顶角相等) CD=BD(中点定义)
∴△ADC≌△EDB(SAS)
(2)探究得出AD的取值范围是1<AD<7;
【感悟】解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AC=BF.
求证:∠BFD=∠CAD.
分析 (1)延长AD到点E,使DE=AD,根据SAS定理证明△ADC≌△EDB;
(2)根据全等三角形的性质得到BE=AC=6,根据三角形三边关系计算;
(3)延长AD到H,使DH=AD,根据全等三角形的性质得到BH=AC,∠BHD=∠CAD,根据等腰三角形的性质证明即可.
解答 (1)证明:∵延长AD到点E,使DE=AD,
在△ADC和△EDB中,
AD=ED,∠ADC=∠EDB(对顶角相等),CD=BD(中点定义),
∴△ADC≌△EDB(SAS),
故答案为:对顶角相等;SAS;
(2)解:∵△ADC≌△EDB,
∴BE=AC=6,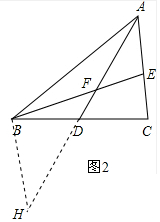
∴AB-BE<AE<AB+BE,即1<AD<7,
故答案为:1<AD<7;
(3)证明:延长AD到H,使DH=AD,
由(1)得,△ADC≌△HDB,
∴BH=AC,∠BHD=∠CAD,
∵AC=BF,
∴BH=BF,
∴∠BFD=∠BHD,
∴∠BFD=∠CAD.
点评 本题考查的是三角形的中线的概念和性质、全等三角形的判定和性质、三角形三边关系,掌握全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
1.在?ABCD中,下列关于向量的等式正确的是( )
| A. | $\stackrel{→}{AB}$+$\stackrel{→}{CD}$=$\stackrel{→}{0}$ | B. | $\stackrel{→}{AB}$-$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | C. | $\stackrel{→}{AB}$+$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | D. | $\stackrel{→}{AB}$+$\stackrel{→}{BD}$=$\stackrel{→}{DA}$ |
5.一种登革热病毒的直径约为0.00000005m,数据0.00000005m可用科学记数法表示为( )
| A. | 5×10-7m | B. | 5×10-8m | C. | 0.5×10-7m | D. | -5×108m |
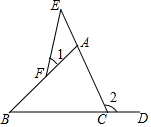 如图所示,∠1,∠2是不是△ABC的外角?图中还有哪些角可以看作一个三角形的外角?
如图所示,∠1,∠2是不是△ABC的外角?图中还有哪些角可以看作一个三角形的外角?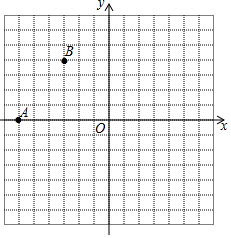 如图,在直角坐标平面内,已知点A的坐标(-6,0).
如图,在直角坐标平面内,已知点A的坐标(-6,0). 解不等式组:$\left\{{\begin{array}{l}{\frac{1-2x}{3}≤x+2}\\{2x+2>2({2x-1})}\end{array}}\right.$.把它的解集在数轴上表示出来,并写出这个不等式组的整数解.
解不等式组:$\left\{{\begin{array}{l}{\frac{1-2x}{3}≤x+2}\\{2x+2>2({2x-1})}\end{array}}\right.$.把它的解集在数轴上表示出来,并写出这个不等式组的整数解.