题目内容
8.当x发生变化时,分式$\frac{3{x}^{2}+6x+5}{\frac{1}{2}{x}^{2}+x+1}$的最小值是4,$\frac{{x}^{2}+2x-2}{{x}^{2}+2x+2}$的最小值为-3.分析 将$\frac{3{x}^{2}+6x+5}{\frac{1}{2}{x}^{2}+x+1}$变形为6-$\frac{1}{\frac{1}{2}{x}^{2}+x+1}$,$\frac{{x}^{2}+2x-2}{{x}^{2}+2x+2}$变形为1$-\frac{4}{{x}^{2}+2x+2}$,然后求得分母的最大值从而可求得答案.
解答 解:$\frac{3{x}^{2}+6x+5}{\frac{1}{2}{x}^{2}+x+1}$=$\frac{3{x}^{2}+6x+6-1}{\frac{1}{2}{x}^{2}+x+1}$=6-$\frac{1}{\frac{1}{2}{x}^{2}+x+1}$,
当x=-$\frac{b}{2a}$=-1时,$\frac{1}{2}{x}^{2}+x+1$有最大值,最大值为$\frac{1}{2}$.
∴6-$\frac{1}{\frac{1}{2}}$=6-2=4.
∴分式$\frac{3{x}^{2}+6x+5}{\frac{1}{2}{x}^{2}+x+1}$的最小值是4.
$\frac{{x}^{2}+2x-2}{{x}^{2}+2x+2}$=$\frac{{x}^{2}+2x+2-4}{{x}^{2}+2x+2}$=1$-\frac{4}{{x}^{2}+2x+2}$,
当x=-1时,x2+2x+2有最小值,最小值为1.
∴1-$\frac{4}{1}$=-3.
∴分式$\frac{{x}^{2}+2x-2}{{x}^{2}+2x+2}$的最小值为-3.
故答案为:4;-3.
点评 本题主要考查的是二次函数的最值,能够将分式进行正确变形是解题的关键.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
19.若某数的平方根为2a+3和a-15,则这个数是( )
| A. | -18 | B. | $-\frac{2}{3}$ | C. | 121 | D. | 以上结论都不是 |
13.要做一个母线10分米,底面圆的直径为3$\frac{1}{3}$分米的圆锥形漏斗(接缝处不计),则需要扇形铁皮的圆心角是( )
| A. | 30° | B. | 60° | C. | 45° | D. | 90° |
20.已知数据:10,8,6,10,8,13,11,10,12,7,9,8,12,9,11,12,9,10,11,10,那么频数为4的一组是( )
| A. | 5.5~7.5 | B. | 7.5~9.5 | C. | 9.5~11.5 | D. | 11.5~13.5 |
17.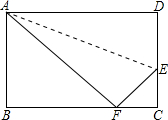 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )
如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |