题目内容
将一个正方体纸盒的某些棱剪开后,可以将其平铺成一个“平面展开图”,也就是由6个正方形连接起来的一整张纸片.那么正方体的平面展开图一共有多少种?请全部画出来.(注意:如果经过旋转或者翻转后,两个展开图可以完全重合,那么只能算作一种平面图形)
考点:作图—应用与设计作图,几何体的展开图
专题:
分析:我们可以逆向思考,若由6个正方形连接起来的一整张纸片能组成正方体之和,则保证有两个底面,四个侧面,据此将六个正方形进行排列即可.
解答:解:答:将一个正方体纸盒的某些棱剪开后,可以将其平铺成一个“平面展开图”,也就是由6个正方形连接起来的一整张纸片.那么正方体的平面展开图一共有11种.
画图如下:

画图如下:

点评:本题主要考查了作图--应用与设计作图,要知道正方体展开图的特征,正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2-2-2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3-3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1-3-2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
一个多项式减去x2-2y2等于x2-2y2,则这个多项式是( )
| A、-2x2+y2 |
| B、x2-2y2 |
| C、2x2-4y2 |
| D、-x2+2y2 |
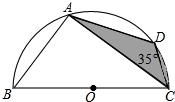 如图,半圆直径BC=10,AB=AD,∠ACD=35°,求阴影部分面积.
如图,半圆直径BC=10,AB=AD,∠ACD=35°,求阴影部分面积. 如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=8,则DG+EH+FI的长是多少?
如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=8,则DG+EH+FI的长是多少? 如图,已知AC∥DE,∠1=∠2,求证:∠B=∠DCE.
如图,已知AC∥DE,∠1=∠2,求证:∠B=∠DCE.



 如图,阴影部分占大正方形的
如图,阴影部分占大正方形的