题目内容
(本题满分6分)已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.

(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
AC=BD
【解析】
试题分析:(1)由于OA=OB,OC=OD,利用等边对等角易得∠A=∠B,∠OCD=∠ODC,而利用三角形外角性质可得∠OCD=∠A+∠AOC,∠ODC=∠BOD+∠B,从而可得∠A+∠AOC=∠BOD+∠B,再利用等量相减,差相等可得∠AOC=∠DOB;
(2)过O作OE⊥AB于E,利用垂径定理有AE=EB,CE=ED,于是AE-CE=BE-DE,即AC=BD.
 试题解析:
试题解析:
(1)∵AO=OB,OC=OD
∴∠A=∠B,∠OCD=∠ODC
∴∠OCA=∠ODC
∴△ACO=△ODB
∴∠AOC=∠DOB
(2)过O作OE⊥AB于E
∴AE=EB,CE=ED
∴AC=BD
考点:等边对等角,三角形外角性质,垂径定理

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 是三角形的三边,则
是三角形的三边,则
 中,∠
中,∠ °,所以
°,所以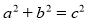
 °,所以
°,所以



 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;

 ,则代数式
,则代数式 ?2x + 4y ? 1的值是__________.
?2x + 4y ? 1的值是__________. x+8分别交x轴、y轴于点A、B,⊙O的半径为2
x+8分别交x轴、y轴于点A、B,⊙O的半径为2 个单位长度.点P为直线y=
个单位长度.点P为直线y=