题目内容
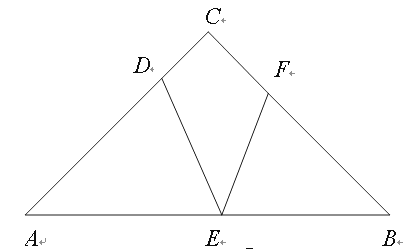
.如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一点,且AD=3cm,动点E从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为x s.作∠DEF=45°,与边BC相交于点F.设BF长为y cm.
cm.
(1)当x= s时,DE ⊥AB;
⊥AB;
(2)求在点E运动过程中,y与x之间的函数关系式及点F运动路线的长;
(3)当△BEF为等腰三角 形
形 时,求x的值.
时,求x的值.


解:(1)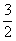

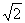
 2分
2分
(2)∵在△ABC中,∠C=90°,AC=B C=4.
C=4.
∴∠A=∠B=45°,AB=4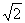
 ,∴∠ADE+∠AED=135°;
,∴∠ADE+∠AED=135°;
又∵∠D EF=45°,∴∠BEF+∠AED=135°,∴∠ADE=∠BEF;
EF=45°,∴∠BEF+∠AED=135°,∴∠ADE=∠BEF;
∴△ADE∽△BEF 4分
∴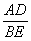
 =
=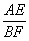
 ,
,
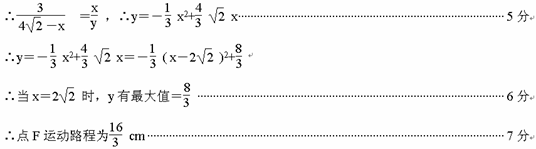

(3)这里有三种情况:
①如图,若EF=BF,则∠B=∠BEF;


又∵△ADE∽△BEF,∴∠A=∠ADE=45°
∴∠AED=90°,∴AE=DE=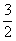

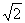
 ,
,
∵动点E的速度为1cm/s ,∴
,∴ 此时x=
此时x=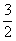

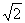
 s;
s;
②如图,若EF=BE,则∠B=∠EFB
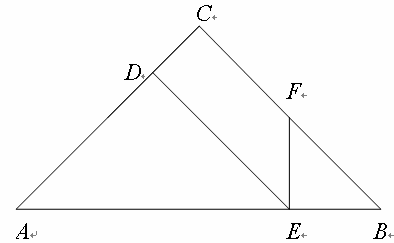

又∵△ADE∽△BEF,∴∠A=∠AED=45°
∴∠ADE=90°,∴AE=3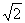
 ,
,
∵动点E的速度为1cm/s
∴此时x=3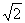
 s;
s;
③如图,若BF=BE,则∠FEB=∠EFB;



练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
 交y轴于点C,对称轴与x轴交于点D, 设点P(x,y)是该抛物线在x轴上方的一个动点(与点C不重合),△PCD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围。
交y轴于点C,对称轴与x轴交于点D, 设点P(x,y)是该抛物线在x轴上方的一个动点(与点C不重合),△PCD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围。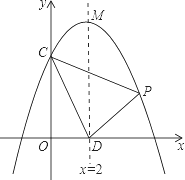
 运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<
运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<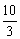
 )秒
)秒

 若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2﹣x1,y2﹣y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标.
若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2﹣x1,y2﹣y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标. 边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.
边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.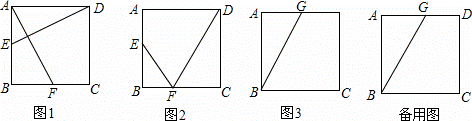


 ?若存在,求出t
?若存在,求出t 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 如图,在平面直角坐标系xOy中,A
如图,在平面直角坐标系xOy中,A (2,0),B(4,0),动点C在直线
(2,0),B(4,0),动点C在直线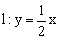 上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是【 】
上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是【 】
 形时,t的值为 秒。
形时,t的值为 秒。

 D.30°
D.30° 数表
数表

 根据表中数的排列规律,则B+D= .
根据表中数的排列规律,则B+D= .