题目内容
3.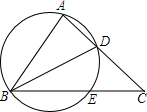 如图,△ABC中,AB=AC,BD是∠ABC的平分线,A、B、D三点的圆与BC相交于点E,你认为AD=CE吗?如果不能,请举反例;如果AD=CE,请说明理由.
如图,△ABC中,AB=AC,BD是∠ABC的平分线,A、B、D三点的圆与BC相交于点E,你认为AD=CE吗?如果不能,请举反例;如果AD=CE,请说明理由.
分析 连结DE,如图,由于∠ABD=∠EBD,根据圆周角定理得到$\widehat{AD}$=$\widehat{DE}$,则AD=DE,再利用∠ABC=∠C,∠CDE=∠ABC得到∠CDE=∠C,所以DE=CE,于是利用等量代换即可得到AD=CE.
解答 解:AD=CE.理由如下:
连结DE,如图,
∵BD是∠ABC的平分线,
∴∠ABD=∠EBD,
∴AD=DE,
∵AB=AC,
∴∠ABC=∠C,
而∠CDE=∠ABC,
∴∠CDE=∠C,
∴DE=CE,
∴AD=CE.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰三角形的判定与性质.

练习册系列答案
相关题目
18.已知$\frac{1}{m}+\frac{2}{m^2}=0$,则m-1=( )
| A. | 0或$-\frac{1}{2}$ | B. | 0或-2 | C. | -2 | D. | $-\frac{1}{2}$ |
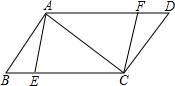 如图,在?ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F在BC、AD上,且BE=DF.
如图,在?ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F在BC、AD上,且BE=DF. 如图,五边形DEFGH是正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙O的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A.
如图,五边形DEFGH是正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙O的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A.