题目内容
7.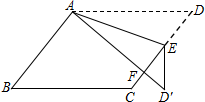 如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=48°,∠DAE=24°,则∠FED'的大小为36°.
如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=48°,∠DAE=24°,则∠FED'的大小为36°.
分析 由平行四边形的性质得出∠D=∠B=48°,由折叠的性质得:∠D′=∠D=48°,∠EAD′=∠DAE=24°,由三角形的外角性质求出∠AEF=72°,与三角形内角和定理求出∠AED′=108°,即可得出∠FED′的大小.
解答 解:∵四边形ABCD是平行四边形,
∴∠D=∠B=48°,
由折叠的性质得:∠D′=∠D=48°,∠EAD′=∠DAE=24°,
∴∠AEF=∠D+∠DAE=48°+24°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
故答案为:36°.
点评 本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AEF和∠AED′是解决问题的关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
12.A,B两地盛产桃,A地有桃400吨,B地有桃300吨.现将这些桃运到C、D两个冷藏仓库,已知C仓库可储存320吨,D仓库可储存380吨;从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从A地运往C仓库的桃重量为x吨,A、B两地运往两仓库的桃运输费用分别为yA元和yB元.
(1)请填写下表后分别求出yA,yB与x之间的函数关系式,并写出定义域.
(2)试讨论A,B两地中,哪个运费较少?
(1)请填写下表后分别求出yA,yB与x之间的函数关系式,并写出定义域.
| 仓库 产地 | C | D | 总计 |
| A | x吨 | 400吨 | |
| B | 300吨 | ||
| 总计 | 320吨 | 380 | 700吨 |
 如图,A、B、C都在⊙O上,∠1=∠B,求证:AE是⊙O的切线.
如图,A、B、C都在⊙O上,∠1=∠B,求证:AE是⊙O的切线. 如图,将长、宽分别为40cm,20cm的长方形玻璃裁成两部分,然后拼成一个直角三角形,画出图形,并注明各边的长度.
如图,将长、宽分别为40cm,20cm的长方形玻璃裁成两部分,然后拼成一个直角三角形,画出图形,并注明各边的长度.