Question

已知四边形ABCD中．E、F分别是AB、AD边上的点，DE与CF交于点G。

   （一）问题初探；  

如图①，若四边形ABCD是正方形，且DE上CF．则DE与’CF的数量关系是   

                   ；

    （二）类比延伸

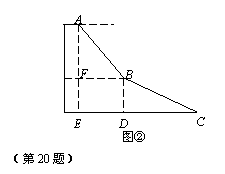
    (1)如图②若四边形ABCD是矩形．AB=m, AD=n．且DE⊥CF，则=           ．（用含m，n的代数式表示）

    (2)如图③，若四边形ABCD是平行四边形，当∠B+∠EGC=180°时,(1)中的结论是否成立，若成立，请证明你的结论；若不成立，请说明理由．

    （三）拓展探究

如图④，若BA= BC= 6,DA= DC= 8,∠BAD= 90°．DE⊥CF，请直接写出的值.

Answer 1

解(1)DE=CF (2)……(4分)

(2)证明如下：

当∠B+∠EGC=180°时，在AD的延长线上取点M，

使CM=CF．则∠CMF=∠CFM.

∵AB∥CD，∴∠A=∠CDM，

∵∠B+∠EGC=180°，

∴∠AED=∠FCB,∴∠CMF=∠AED.

∴△ADE∽△DCM，∴，即………（8分）

(3)………(10分)