题目内容
已知函数y=(m+2)xm2+m-4-8x+10是关于x的二次函数,求:
(1)当m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(2)当m为何值时,抛物线有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
(1)当m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(2)当m为何值时,抛物线有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
考点:二次函数的最值,二次函数的定义
专题:
分析:根据二次函数的定义列出方程求解x,再根据二次函数的最值问题和增减性对两个小题解答即可.
解答:解:由题意得,m2+m-4=2,
m2+m-6=0,
解得m1=2,m2=-3,
(1)m=2时,m+2=2+2=4>0,抛物线有最低点,
此时,y=4x2-8x+10=4(x-1)2+6,
所以,最低点是(1,6),
当x>1时,y随x的增大而增大;
(2)m=-3时,m+2=-3+2=-1,抛物线有最大值,
此时,y=-x2-8x+10=-(x+4)2+26,
所以,最大值为26,
当x>-4时,y随x的增大而减小.
m2+m-6=0,
解得m1=2,m2=-3,
(1)m=2时,m+2=2+2=4>0,抛物线有最低点,
此时,y=4x2-8x+10=4(x-1)2+6,
所以,最低点是(1,6),
当x>1时,y随x的增大而增大;
(2)m=-3时,m+2=-3+2=-1,抛物线有最大值,
此时,y=-x2-8x+10=-(x+4)2+26,
所以,最大值为26,
当x>-4时,y随x的增大而减小.
点评:本题考查了二次函数的最值问题,二次函数的定义,二次函数的增减性,熟练掌握二次函数的性质是解题的关键,把函数解析式整理成顶点式形式求解更简便.

练习册系列答案
相关题目
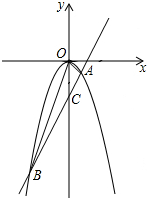 已知函数y=ax2(a≠0)与直线y=2x-3交于A(1,b)和点B,求S△ABO.
已知函数y=ax2(a≠0)与直线y=2x-3交于A(1,b)和点B,求S△ABO. 请指出下面正方体展开图中任何一个面的对面是哪一个?
请指出下面正方体展开图中任何一个面的对面是哪一个?