题目内容
10.一次函数y=kx+b(k≠0)的图象经过A(-1,-4),B(2,2)两点,P为反比例函数y=$\frac{kb}{x}$图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为( )| A. | 2 | B. | 4 | C. | 8 | D. | 不确定 |
分析 根据待定系数法,可得k,b,根据反比例函数图象上的点垂直于坐标轴得到的三角形的面积等于|k|的一半,可得答案.
解答 解:将A(-1,-4),B(2,2)代入函数解析式,得
$\left\{\begin{array}{l}{-k+b=-4}\\{2k+b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=-2}\end{array}\right.$,
P为反比例函数y=$\frac{kb}{x}$图象上一动点,
反比例函数的解析式y=$\frac{-4}{x}$,
P为反比例函数y=$\frac{kb}{x}$图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,
则△PCO的面积为$\frac{1}{2}$|k|=2,
故选:A.
点评 本题考查了反比例函数图象上点的坐标特征,利用反比例函数图象上的点垂直于坐标轴得到的三角形的面积等于|k|的一半

练习册系列答案
相关题目
5.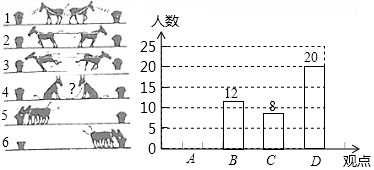 主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重;
B.放下利益,彼此平衡;
C.放下性格,彼此成就;
D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如图两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
(1)参加本次讨论的学生共有50人;
(2)表中a=10,b=0.16;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.
 主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:A.放下自我,彼此尊重;
B.放下利益,彼此平衡;
C.放下性格,彼此成就;
D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如图两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
| 观点 | 频数 | 频率 |
| A | a | 0.2 |
| B | 12 | 0.24 |
| C | 8 | b |
| D | 20 | 0.4 |
(2)表中a=10,b=0.16;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.
19.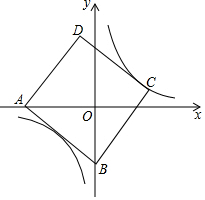 如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )
如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )
 如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )
如图,正方形ABCD的边长为5,点A的坐标为(-4,0),点B在y轴上,若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点C,则该反比例函数的表达式为( )| A. | y=$\frac{3}{x}$ | B. | y=$\frac{4}{x}$ | C. | y=$\frac{5}{x}$ | D. | y=$\frac{6}{x}$ |
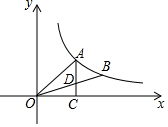 如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若D为OB的中点,△ADO的面积为3,则k的值为8.
如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若D为OB的中点,△ADO的面积为3,则k的值为8.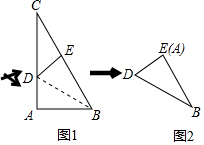 在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.
在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),减去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为40或$\frac{80\sqrt{3}}{3}$cm.