题目内容
已知2m2-3m-1=0,n2+3n-2=0,mn≠1,则m2+
= .
| 1 |
| n2 |
考点:根与系数的关系
专题:计算题
分析:先把n2+3n-2=0变形为2•(
)2-3•
-1=0,由于2m2-3m-1=0,mn≠1,所以m与
可看作为方程2x2-3x-1=0的两根,根据根与系数的关系得m+
=
,m•
=-
,再利用完全平方公式把m2+
变形为(m+
)2-2m•
,然后利用整体代入的方法计算.
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| 3 |
| 2 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n2 |
| 1 |
| n |
| 1 |
| n |
解答:解:∵n2+3n-2=0,
∴n≠0,
∴2•(
)2-3•
-1=0,
而2m2-3m-1=0,mn≠1,
∴m与
可看作为方程2x2-3x-1=0的两根,
∴m+
=
,m•
=-
,
∴m2+
=(m+
)2-2m•
=
-2×(-
)=
.
故答案为
.
∴n≠0,
∴2•(
| 1 |
| n |
| 1 |
| n |
而2m2-3m-1=0,mn≠1,
∴m与
| 1 |
| n |
∴m+
| 1 |
| n |
| 3 |
| 2 |
| 1 |
| n |
| 1 |
| 2 |
∴m2+
| 1 |
| n2 |
| 1 |
| n |
| 1 |
| n |
| 9 |
| 4 |
| 1 |
| 2 |
| 13 |
| 4 |
故答案为
| 13 |
| 4 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在频数分布直方图中,各个小长方形的高( )
| A、与频数成正比 |
| B、与频数成反比 |
| C、与频数不成正比也不成反比 |
| D、与频数无关 |
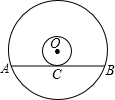 如图所示是一张电脑光盘的表面,两个圆的圆心是点O,大圆的弦AB所在直线是小圆的切线,弦AB=4
如图所示是一张电脑光盘的表面,两个圆的圆心是点O,大圆的弦AB所在直线是小圆的切线,弦AB=4 如图,△ABC中,AD平分∠BAC,若AB+BD=AC,则∠B:∠C=
如图,△ABC中,AD平分∠BAC,若AB+BD=AC,则∠B:∠C=