题目内容
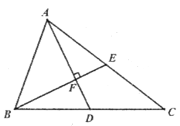
【题目】如图,在![]() 中,AC、BC边上的中线BE、AD交于点
中,AC、BC边上的中线BE、AD交于点![]() ,且
,且![]() ,AC=20,AD=12.
,AC=20,AD=12.
(1)求![]() 的长.
的长.
(2)求![]() 的余弦值.
的余弦值.
【答案】(1)![]() 的长为18;(2)
的长为18;(2)![]() 的余弦值为
的余弦值为![]() .
.
【解析】
由BE、AD是AC、BC的中线,根据重心的性质可得AF=![]() AD,BE=2EF,即可求出AF的长,利用勾股定理可求出EF的长,进而求出BF的长,利用BE=BF+EF即可得答案;(2)利用勾股定理可求出AB的长,根据余弦的定义即可得答案.
AD,BE=2EF,即可求出AF的长,利用勾股定理可求出EF的长,进而求出BF的长,利用BE=BF+EF即可得答案;(2)利用勾股定理可求出AB的长,根据余弦的定义即可得答案.
(1)∵中线BE、AD交于点![]()
∴点![]() 是
是![]() 的重心,
的重心,
∴AF=![]() AD,BE=2EF,
AD,BE=2EF,
∵AD=12,
∴AF=8,
∴DF=AD-AF=12-8=4,
∵BE是边![]() 的中线,
的中线,
∴![]() ,
,
∵AD⊥BE,
∴EF=![]() =
=![]() =6,
=6,
∴BF=2EF=12,
∴BE=BF+EF=18.
(2)在![]() 中,
中,![]() ,
,
∴![]()
∴![]()

练习册系列答案
相关题目