题目内容
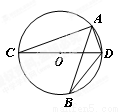
维修人员为更换一圆柱形的输水管道，需先确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面，若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径.
【解析】
过点O作OC⊥AB于D，交⊙O于C，连接OB，
∵OC⊥AB
∴BD=
AB=
×16=8cm
由题意可知，CD=4cm
∴设半径为xcm，则OD=（x﹣4）cm
在Rt△BOD中，
由勾股定理得：
即
解得：x=10．
答：这个圆形截面的半径为10cm
【解析】
试题分析：先过点O作OC⊥AB于D，交⊙O于C，连接OB，得出BD=
AB，再设半径为xcm，则OD=（x﹣4）cm，根据
，得出
，再求出x的值即可
考点：垂径定理的应用；勾股定理
练习册系列答案
相关题目
对于抛物线 
.
（1）它与x轴交点的坐标为 ，与y轴交点的坐标为 ，顶点坐标为 ；
（2）在坐标系中利用描点法画出此抛物线；
x | … | … | |||||
y | … | … |
（3）利用以上信息解答下列问题：若关于x的一元二次方程
（t为实数）在
＜x＜
的范围内有解，则t的取值范围是 ．
（千克）与销售价
（元/千克）有如下关系:
.设这种商品的销售利润为
（元）.
与
之间的函数关系式；
在反比例函数
的图象上，
轴于点
，
的面积为3，则
．
，则较大三角形的面积是（ ）
B． 65
（0°＜
开始，用等长的小棒依次向右摆放，其中
为第一根小棒，且
.
的式子表示）