��Ŀ����
ij�̳�����һ�ֳɱ�Ϊ20Ԫ����Ʒ���г����鷢��,����Ʒÿ��������� ��ǧ�ˣ������ۼ�
��ǧ�ˣ������ۼ� ��Ԫ/ǧ�ˣ������¹�ϵ:
��Ԫ/ǧ�ˣ������¹�ϵ: .��������Ʒ����������Ϊ
.��������Ʒ����������Ϊ ��Ԫ��.
��Ԫ��.
��1���� ��
�� ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2���ڲ�������ǰ����,���ۼ���ʲô��Χ��ÿ��������������ۼ����Ӷ�����?��������Ƕ���?
��3�������۲��Ź涨���ֲ�Ʒ�����ۼ۲��ø���28Ԫ/ǧ��,��ũ����Ҫÿ����150Ԫ����������,���ۼ�Ӧ��Ϊ����Ԫ?
��������
��1��y=��x��20��w
=��x��20������2x+80��
= ��
��
��y��x�ĺ�����ϵʽΪ��
��2��
����ڲ�������ǰ�����ۼ���20��30Ԫʱ��ÿ��������������ۼ۵����Ӷ����ӣ�
�൱x=30ʱ��y�����ֵ200��
�൱���ۼ۶�Ϊ30Ԫ/ǧ��ʱ��ÿ��ɻ������������200Ԫ
��3����y=150ʱ���ɵ÷��̣�
 ��
��
���x1=25��x2=35
�������⣬x2=35�������⣬Ӧ��ȥ��
�൱���ۼ۶�Ϊ25Ԫ/ǧ��ʱ����ũ��ÿ��ɻ����������150Ԫ
��������
������������ݡ�����=�ۼ۩����ۡ��������y��x֮��ĺ�����ϵʽ��Ȼ�����ú�����������ȷ�����������
���㣺���κ�����Ӧ��

��ϰ��ϵ�д�
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
�����Ŀ
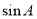 ��
�� B��
B��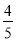 C��
C��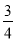 D��
D��
 ��
�� ��ֻ��һ�������㣬��
��ֻ��һ�������㣬�� ��ֵΪ ��
��ֵΪ ��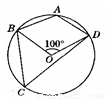



 ,
,  , 0�У���ʽ�ĸ����У�����
, 0�У���ʽ�ĸ����У�����