题目内容
7.已知二次函数y=(m-1)x2+2mx+(m+3).(1)如果该二次函数的图象与x轴无交点,求m的取值范围;
(2)在(1)的前提下如果m取最小的整数,求此二次函数表达式.
分析 (1)根据二次函数的图象与x轴无交点,可得△<0且m-1≠0;
(2)根据题意和(1)的结果可得m的值,代入即可.
解答 解:(1)∵二次函数y=(m-1)x2+2mx+(m+3)的图象与x轴无交点,
∴△=4m2-4(m-1)(m+3)<0且m-1≠0,
解得$m>\frac{3}{2}$;
(2)根据题意得,解得m=2.
∴二次函数的表达式是y=x2+4x+5.
点评 本题考查了抛物线与x轴的交点,关键是掌握当△=b2-4ac>0时图象与x轴有两个交点;当△=b2-4ac=0时图象与x轴有一个交点;当△=b2-4ac<0时图象与x轴没有交点.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
16.在解方程$\frac{1-2x}{3}$=1-$\frac{3x+1}{6}$时要先去分母,则下列去分母中正确的是( )
| A. | 2-4x=1-3x+1 | B. | 2(1-2x)=1-(3x+1) | C. | 2-4x=6-3x+1 | D. | 2(1-2x)=6-(3x+1) |
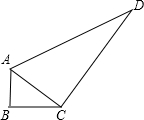 一块钢板形状如图所示,量得AB=3,BC=4,AC=5,CD=12,AD=13,请你计算一下这块钢板的面积.
一块钢板形状如图所示,量得AB=3,BC=4,AC=5,CD=12,AD=13,请你计算一下这块钢板的面积.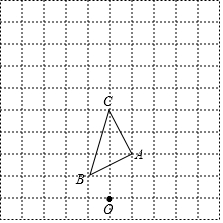 如图,在边长为1个单位长度的小正方形组成的网格中.
如图,在边长为1个单位长度的小正方形组成的网格中.