题目内容
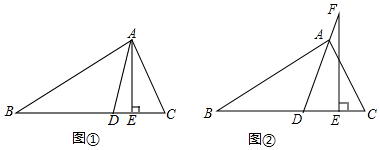
4.如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
分析 (1)先根据三角形内角和定理求出∠BAC的度数,再由角平分线的定义得出∠BAD的度数,再由AE⊥BC得出∠AEB=90°,进而可得出结论;
(2)同(1),可得∠ADE=75°,再由FE⊥BC可知∠FEB=90°,根据∠DFE=90°-∠ADE可得出结论.
解答 解(1)∵∠B=40°,∠C=70°,
∴∠BAC=70°.
∵CF平分∠DCE,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°.
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°-∠ADE=15°;
(2)同(1),可得∠ADE=75°.
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°-∠ADE=15°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
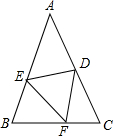 如图,已知△ABC中,AB=AC=6,BC=4,点D,E,F分别在AC,AB,BC边上,△BEF沿着直线EF翻折后与△DEF重合,若△DFC与△ABC相似,则CD的长为$\frac{6}{5}$或$\frac{4}{5}$.
如图,已知△ABC中,AB=AC=6,BC=4,点D,E,F分别在AC,AB,BC边上,△BEF沿着直线EF翻折后与△DEF重合,若△DFC与△ABC相似,则CD的长为$\frac{6}{5}$或$\frac{4}{5}$. 如图,∠BDC=2∠ACB,CE=BD,EF∥AB,求证:AB=FB.
如图,∠BDC=2∠ACB,CE=BD,EF∥AB,求证:AB=FB.