题目内容
 已知:如图,点B是AD的中点,点E是AB的中点,AB=AC 求证:CE=
已知:如图,点B是AD的中点,点E是AB的中点,AB=AC 求证:CE=| 1 |
| 2 |
考点:三角形中位线定理,全等三角形的判定与性质
专题:证明题
分析:如图,作辅助线,首先证明∠FBC=∠EBC,BF=BE;进而证明△EBC≌△FBC,得到CE=CF,问题即可解决.
解答: 证明:如图,取DC的中点F,连接BF;
证明:如图,取DC的中点F,连接BF;
∵点B是AD的中点,
∴BF为△ADC的中位线,
∴BF∥AC,且BF=
AC;
∴∠ACB=∠FBC,而AB=AC,
∴∠ABC=∠ACB,
∴∠FBC=∠EBC;
又∵点E是AB的中点,AB=AC,
∴BE=
AC,BF=BE;
在△EBC与△FBC中,
,
∴△EBC≌△FBC(SAS),
∴CE=CF,而CF=
CD,
∴CE=
CD.
 证明:如图,取DC的中点F,连接BF;
证明:如图,取DC的中点F,连接BF;∵点B是AD的中点,
∴BF为△ADC的中位线,
∴BF∥AC,且BF=
| 1 |
| 2 |
∴∠ACB=∠FBC,而AB=AC,
∴∠ABC=∠ACB,
∴∠FBC=∠EBC;
又∵点E是AB的中点,AB=AC,
∴BE=
| 1 |
| 2 |
在△EBC与△FBC中,
|
∴△EBC≌△FBC(SAS),
∴CE=CF,而CF=
| 1 |
| 2 |
∴CE=
| 1 |
| 2 |
点评:该题考查了三角形的中位线定理及全等三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造全等三角形,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
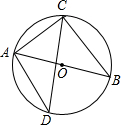 如图,AB是⊙O的直径,弦AC=12cm,BC=16cm,点D在⊙O上且与点C位于AB异侧,当AD=
如图,AB是⊙O的直径,弦AC=12cm,BC=16cm,点D在⊙O上且与点C位于AB异侧,当AD=