题目内容
4.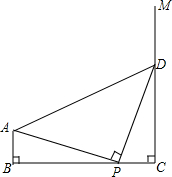 如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的点,过点P作DP⊥AP交射线CM于点D,连结AD.若BP=3,则△ABP的周长为4+$\sqrt{10}$.
如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的点,过点P作DP⊥AP交射线CM于点D,连结AD.若BP=3,则△ABP的周长为4+$\sqrt{10}$.
分析 先根据勾股定理求出AP,即可得出结果.
解答 解:∵AB⊥BC,
∴∠B=90°,
∴AP=$\sqrt{A{B}^{2}+B{P}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴△ABP的周长=AB+BP+AP=1+3+$\sqrt{10}$=4+$\sqrt{10}$;
故答案为:4+$\sqrt{10}$.
点评 本题考查了勾股定理的运用以及周长的计算;运用勾股定理求出边长是解决问题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
14. 如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
 如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 65° |
15.下列函数中,一次函数有( )
| A. | y=-8x | B. | y=$\frac{-8}{x}$ | C. | y=-8x2+6 | D. | y=-0.5x-1 |
12.下列运算中正确的是( )
| A. | a+a=a2 | B. | a•a2=a2 | C. | (ab)2=a2b2 | D. | (a2)3=a5 |
16.△ABC中,∠C=90°,∠A:∠B=2:3,则∠A的度数为( )
| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
