题目内容
14.一透明的敞口正方体容器ABCD-A′B′C′D′装有一些液体,棱AB始终在水平桌面上,如图①,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图②.则液体的体积为24dm3.
分析 首先根据水面与水平面平行可以得到CQ与BE平行,利用勾股定理即可求得BQ的长,由题意可知液体正好是一个以△BCQ是底面的直棱柱,据此即可求得液体的体积.
解答 解:∵CQ=5dm,BC=4dm,
∴BQ=$\sqrt{{5}^{2}-{4}^{2}}$=3dm,
∴液体的体积为:V液=$\frac{1}{2}$×3×4×4=24(dm3).
故答案为:24dm3.
点评 本题考查了四边形的体积计算以及三视图的认识和勾股定理的运用,正确理解棱柱的体积的计算是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.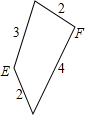 已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
 已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )
已知有一块等腰三角形纸板,在它的两腰上各有一点E和F,把这两点分别与底边中点连结,并沿着这两条线段剪下两个三角形,所得的这两个三角形相似,剩余部分(四边形)的四条边的长度如图所示,那么原等腰三角形的底边长为( )| A. | $\frac{4}{3}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{3}$或$\frac{24}{5}$ | D. | $\frac{2}{3}$或$\frac{12}{5}$ |
3.不等式x>-1在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
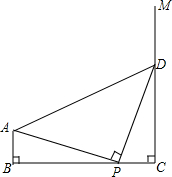 如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的点,过点P作DP⊥AP交射线CM于点D,连结AD.若BP=3,则△ABP的周长为4+$\sqrt{10}$.
如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的点,过点P作DP⊥AP交射线CM于点D,连结AD.若BP=3,则△ABP的周长为4+$\sqrt{10}$.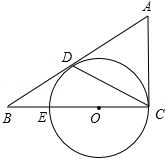 如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.