题目内容
14.将正面分别标有数字3,5,6,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上.(1)随机地抽取一张,求P(奇数);
(2)随机地抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,请用树状图(或列表)的方法,求恰好为“56”的概率.
分析 (1)直接根据概率公式求解;
(2)画树状图展示所有6种等可能的结果数,得到“56”的结果数为1,然后根据概率公式求解.
解答 解:(1)随机抽取一张卡片,抽到一张的数字可能为3,5,6,共3种,它们出现的可能性相等,因此
P(奇数)=$\frac{2}{3}$;
(2)画出树状图如下:
共有6种等可能的结果数,它们是53,63,35,65,36,56,其中恰好为“56”的结果数为1,
所以P(恰好为56)=$\frac{1}{6}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
相关题目
9.若x=-$\frac{3}{5}$是关于x的方程5x-m=0的解,则m的值为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -3 | D. | -$\frac{1}{3}$ |
19.下列四组变形中,正确的是( )
| A. | 由2x-3=1,得2x=1-3 | B. | 由-2x=1,得x=-2 | ||
| C. | 由2(x-3)=1,得2x-3=1 | D. | 由8-x=x-5,得-x-x=-5-8 |
6.下列计算正确的是( )
| A. | (4a)2=8a2 | B. | 3a2•2a3=6a6 | C. | (a3)8=(a6)4 | D. | (-a)3÷(-a)2=a |
3. 如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥x轴,交双曲线y=-$\frac{3}{x}$(x<0)于点B,若OA⊥OB,则$\frac{OA}{OB}$的值为( )
如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥x轴,交双曲线y=-$\frac{3}{x}$(x<0)于点B,若OA⊥OB,则$\frac{OA}{OB}$的值为( )
 如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥x轴,交双曲线y=-$\frac{3}{x}$(x<0)于点B,若OA⊥OB,则$\frac{OA}{OB}$的值为( )
如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥x轴,交双曲线y=-$\frac{3}{x}$(x<0)于点B,若OA⊥OB,则$\frac{OA}{OB}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
 如图,直线AB,CD相交于点O,OE平分∠BOD,若∠AOE=144°,则∠AOC的度数是72°.
如图,直线AB,CD相交于点O,OE平分∠BOD,若∠AOE=144°,则∠AOC的度数是72°.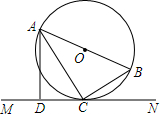 如图,AB是⊙O的直径,C是⊙O上一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.求证:MN是⊙O的切线.
如图,AB是⊙O的直径,C是⊙O上一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.求证:MN是⊙O的切线.