题目内容
12.甲,乙两人两次同时在同一家超市购买糖果,两次购买糖果的价格分别是每千克a元和b元(a≠b),甲每次购买10千克糖果,乙每次花10元钱购买糖果.(1)甲两次购买糖果共付款10(a+b)元,乙两次共购买($\frac{10}{a}$+$\frac{10}{b}$)千克糖果(用含a,b的代数式表示);
(2)请你判断甲,乙两人的购买方式哪一种购买的平均价格更低?请说明理由.
分析 (1)利用两次购买糖果的价格以及购买的质量与钱数得出即可;
(2)根据总钱数除以总千克数求出甲乙两人买糖果的平均价格,利用作差法比较即可.
解答 解:(1)∵两次购买糖果的价格分别是每千克a元和b元(a≠b),甲每次购买10千克糖果,
∴甲两次购买糖果共付款:10(a+b)元,
∵两次购买糖果的价格分别是每千克a元和b元(a≠b),乙每次花10元钱购买糖果,
∴乙两次共购买($\frac{10}{a}$+$\frac{10}{b}$)千克糖果;
故答案为:10(a+b),($\frac{10}{a}$+$\frac{10}{b}$);
(2)根据题意得:甲买糖果的平均价格为$\frac{10a+10b}{20}$=$\frac{a+b}{2}$(元);
乙买糖果的平均价格为$\frac{20}{\frac{10}{a}+\frac{10}{b}}$=$\frac{2ab}{a+b}$(元),
∵$\frac{a+b}{2}$-$\frac{2ab}{a+b}$=$\frac{(a+b)^{2}-4ab}{2(a+b)}$=$\frac{(a-b)^{2}}{2(a+b)}$≥0,
∴乙买糖果的平均价格低.
点评 此题考查了分式的混合运算,弄清平均价格=$\frac{总钱数}{总千克数}$是解本题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
3. 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )| A. | 34° | B. | 36° | C. | 38° | D. | 40° |
7.已知关于x的分式方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=0有增根,则m=( )
| A. | 0 | B. | -4 | C. | 2或1 | D. | 0或-4 |
4.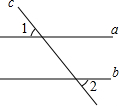 已知:如图,直线a∥b,若∠1=66°,则∠2的度数为( )
已知:如图,直线a∥b,若∠1=66°,则∠2的度数为( )
 已知:如图,直线a∥b,若∠1=66°,则∠2的度数为( )
已知:如图,直线a∥b,若∠1=66°,则∠2的度数为( )| A. | 66° | B. | 68° | C. | 76° | D. | 89° |
1.用一副三角尺,你能画出下面那个度数的角( )
| A. | 65度 | B. | 105度 | C. | 85度 | D. | 95度 |
2.计算20152-2014×2016的结果是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
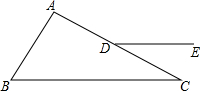 如图,△ABC中,∠A=90°,点D在AC边上,DE∥BC.若∠ADE=139°,则∠B的度数是49°.
如图,△ABC中,∠A=90°,点D在AC边上,DE∥BC.若∠ADE=139°,则∠B的度数是49°.