Question

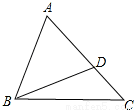
如图，三角板ABC中，∠ACB=90°，AB=2，∠A=30°，三角板ABC绕直角顶点C顺时针旋转90°得到△A1B1C，求：

（1）的长；

（2）在这个旋转过程中三角板AC边所扫过的扇形ACA1的面积；

（3）在这个旋转过程中三角板所扫过的图形面积．

Answer 1

（1） ；（2） ；（3） ．

【解析】

试题分析：（1）由三角板ABC中，∠ACB=90°，AB=2，∠A=30°，可求得BC的长，继而求得AC的长，然后利用弧长公式，即可求得的长；

（2）直接利用扇形的面积公式求解即可求得答案；

（3）由三角板所扫过的图形面积=S扇形BCD+S扇形ACA1+S△ACD，即可求得答案．

试题解析：（1）∵∠ACB=90°，AB=2，∠A=30°，

∴BC=AB=×2=1，

根据勾股定理，AC=，

∴的长=；

（2）扇形ACA1的面积=；

（3）设与AB相交于D，

∵∠ACB=90°，∠A=30°，

∴∠B=90°-30°=60°，

又∵BC=CD，

∴△BCD是等边三角形，

∴BD=BC=1，

∴AD=AB-BD=2-1=1，

∴S△ACD=S△ABC=××1×=，

∴三角板所扫过的图形面积=S扇形BCD+S扇形ACA1+S△ACD

=

=．

考点：1．旋转的性质；2．勾股定理；3．扇形面积的计算．