题目内容
5.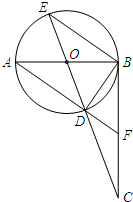 如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.
如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.(1)试判断∠CBD与∠CEB是否相等,并证明你的结论;
(2)求证:$\frac{BD}{BE}=\frac{CD}{BC}$;
(3)若$\frac{BC}{AB}=\frac{3}{2}$,求tan∠E的值.
分析 (1)根据题意即可推出∠CBD=∠BAD,由∠BAD=∠CEB,即可推出∠CBD与∠CEB相等;
(2)根据(1)所推出的结论,通过求证△EBC∽△BDC,即可推出结论;
(3)通过设AB=2a,则BC=3a,根据题意,推出OC的长度,然后通过正确函数的定义求得正切值即可.
解答 解:(1)∠CBD与∠CEB相等.
证明:∵BC⊥AB,∠CBD与∠2互余,∠CEB=∠EBO与∠2互余,
∴∠CBD=∠CEB;
(2)由(1)∠CBD=∠CEB,∠C是公共角,
∴△BCE∽△DCB,
∴对应边成比例:$\frac{BD}{BE}$=$\frac{CD}{BC}$;
(3)∵在Rt△DEB中tan∠E=$\frac{BD}{BE}$,且由(2)$\frac{BD}{BE}$=$\frac{CD}{BC}$,
∵BC=$\frac{3}{2}$AB,可设AB=2a,则BC=3a,而CD=OC-OD,
∴在Rt△OBC中根据勾股定理,OC=$\sqrt{{a^2}+{{(3a)}^2}}$=$\sqrt{10}a$,
∴CD=$\sqrt{10}a$-a,
∴得tan∠E=$\frac{CD}{BC}$=$\frac{{\sqrt{10}-1}}{3}$.
点评 本题主要考查切线的性质、相似三角形的判定与性质、圆周角定理、锐角三角函数定义等知识点,关键在于:(1)熟练运用圆周角定理,切线的性质;(2)根据(1)的结论和已知条件推出△EBC∽△BDC;

练习册系列答案
相关题目
16.2sin30°-tan45°的值等于( )
| A. | $\sqrt{3}-1$ | B. | $\sqrt{2}-1$ | C. | 0 | D. | $-\frac{1}{2}$ |
13.下列运算正确的是( )
| A. | b3•b3=2b3 | B. | $\sqrt{{2}^{2}}$=±2 | C. | (a4)2÷a2=a6 | D. | $\root{3}{-27}$=3 |
17.下列各式中,正确的是( )
| A. | 3$\sqrt{2}-\sqrt{2}$=2 | B. | $\sqrt{8}=4\sqrt{2}$ | C. | ${({\sqrt{-5}})^2}$=5 | D. | $\sqrt{{{(-5)}^2}}$=-5 |
15.小亮问老师有多少岁了,老师说:“我像你这么大时,你才4岁,你到我这么大时,我就40岁了.”求小亮和老师的岁数各是多少?若设小亮和老师的岁数分别为x岁和y岁,则可列方程组( )
| A. | $\left\{\begin{array}{l}{x-4=y-x}\\{y-x=40-y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=4}\\{x+y=40}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-4=y}\\{y-40=x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-4=x-y}\\{y-x=y-40}\end{array}\right.$ |
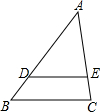 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若$\frac{AE}{AC}$=$\frac{3}{4}$,AD=9,则AB等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若$\frac{AE}{AC}$=$\frac{3}{4}$,AD=9,则AB等于( )