Question

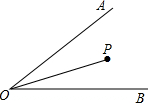如图所示，已知∠AOB为30°，点P在∠AOB内部，OP为10厘米，试在AOB两边上各找一点Q，R（均不与点O重合），求PR+PQ+QR的最小值．

Answer 1

考点：轴对称-最短路线问题

专题：

分析：分别作点P关于OA、OB的对称点P₁、P₂，连P₁、P₂，交OA于Q，交OB于R，△PQR的周长=P₁P₂，然后证明△OP₁P₂是等边三角形，即可求解．

解答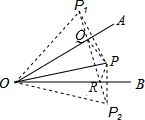：解：分别作点P关于OA、OB的对称点P₁、P₂，连P₁、P₂，交OA于Q，交OB于R，
则OP₁=OP=OP₂，∠P₁OA=∠POA，∠POB=∠P₂OB，
QP=P₁Q，PR=P₂R，则PR+PQ+QR的最小值=△PQR的周长的最小值=P₁P₂
∴∠P₁OP₂=2∠AOB=60°，
∴△OP₁P₂是等边三角形．
△PMN的周长=P₁P₂，
∴PR+PQ+QR的最小值=P₁P₂=OP₁=OP₂=OP=10．

点评：本题考查了对称点的性质，正确正确作出辅助线，证明△OP₁P₂是等边三角形是关键．