题目内容
5. 如图,在△ABC中,AB=AC,AE=AF,BF与CE相交于D.
如图,在△ABC中,AB=AC,AE=AF,BF与CE相交于D.(1)求证:△AEC≌△AFB;
(2)求证:ED=FD.
分析 (1)根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的判定和性质即可得到结论.
解答 证明:(1)在△AEC与△AFB中,$\left\{\begin{array}{l}{AB=AC}\\{∠A=∠A}\\{AE=AF}\end{array}\right.$,
∴△AEC≌△AFB;
(2)∵△AEC≌△AFB,
∴∠FCD=∠EBD,
∵AB=AC,AE=AF,
∴BE=CF,
在△EDB与△FDC中,$\left\{\begin{array}{l}{∠EBD=∠FCD}\\{BE=CF}\\{∠EBD=∠FCD}\\{\;}\end{array}\right.$,
∴△EBD≌△FDC,
∴ED=FD.
点评 本题考查了全等三角形的性质和判定,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
15.△ABC与△DEF的相似比为1:3,则△ABC和△DEF的面积比为( )
| A. | 1:$\sqrt{3}$ | B. | $\sqrt{3}$:1 | C. | 9:1 | D. | 1:9 |
20.单项式-$\frac{5x{y}^{2}}{3}$的系数与次数分别是( )
| A. | -5,2 | B. | -$\frac{1}{3}$,3 | C. | -$\frac{5}{3}$,2 | D. | -$\frac{5}{3}$,3 |
 将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示从上到下第m排,从左到右第n个数,如(4,2)表示整数8,则(11,5)表示的数是60.
将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示从上到下第m排,从左到右第n个数,如(4,2)表示整数8,则(11,5)表示的数是60.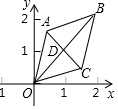 如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第50秒时,菱形的对角线交点D的坐标为(-1,1).
如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第50秒时,菱形的对角线交点D的坐标为(-1,1).