题目内容
16. “一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.
“一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.
设物品的重量为x千克,甲、乙公司快递该物品的费用分别为y甲,y乙.
(1)写出y乙与x的函数表达式;
(2)图中给出了y甲与x的函数图象,请在图中画出(1)中的函数图象;
(3)小丝需要快递的物品重量为4千克,如果想节省快递费用,结合图象指出,应选择的快递公司是甲.
分析 (1)根据乙公司的快递费用=7×物品重量+10,即可得出y乙与x的函数表达式;
(2)根据一次函数图象上点的坐标特征找出y乙与x的函数图象经过的两点,描点、连点成线,即可画出(1)中的函数图象;
(3)根据数量关系找出y甲与x的函数表达式,令y甲=y乙求出费用相等时x的值,结合函数图象即可找出结论.
解答 解:(1)根据题意可知:y乙与x的函数表达式为:y乙=7x+10.
(2)当x=0时,y乙=7x+10=10;
当x=1时,y乙=7x+10=17.
描点、连点成线,画出函数图象,如图所示.
(3)根据题意可知:y甲与x的函数表达式为:y甲=$\left\{\begin{array}{l}{20(0<x≤1)}\\{4x+16(x>1)}\end{array}\right.$.
当y甲=y乙时,有7x+10=4x+16,
解得:x=2.
观察函数图象可知:当x>2时,y甲与x的函数图象在y乙与x的函数图象的下方,
∴当x=4时,选择甲公司费用较低.
故答案为:甲.
点评 本题考查了一次函数的应用、一次函数的图象以及一次函数图象上点的坐标特征,解题的关键是:(1)根据数量关系,找出y乙与x的函数表达式;(2)利用一次函数图象上点的坐标特征找出y乙与x的函数图象经过的两点坐标;(3)观察函数图象解决问题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
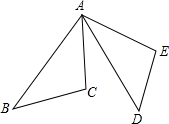 如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗?
如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗? 如图,直线AB∥CD,E是直线CD上一点,过点E作EF⊥AE,垂足为E,交AB于点G,若∠A=36°,求∠DEF的度数.
如图,直线AB∥CD,E是直线CD上一点,过点E作EF⊥AE,垂足为E,交AB于点G,若∠A=36°,求∠DEF的度数.
