题目内容
已知抛物线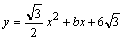 经过
经过
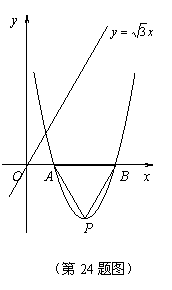
A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线 y=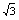 x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;
x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
 |
解:(1)由于抛物线 经过A(2,0),
经过A(2,0),
所以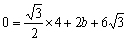 ,
,
解得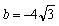 .
.
所以抛物线的解析式为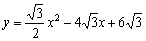 . (*)
. (*)
将(*)配方,得 ,
,
所以顶点P的坐标为(4,-2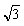
令y=0,得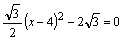 ,
,
解得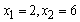 . 所以点B的坐标是(6,0).
. 所以点B的坐标是(6,0).
(2)在直线 y=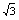 x上存在点D,使四边形OPBD为平行四边形.
x上存在点D,使四边形OPBD为平行四边形.
理由如下:
设直线PB的解析式为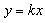 +b,把B(6,0),P(4,-2
+b,把B(6,0),P(4,-2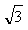 )分别代入,得
)分别代入,得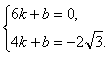 解得
解得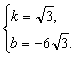
所以直线PB的解析式为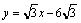
又直线OD的解析式为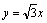
所以直线PB∥OD.
设设直线OP的解析式为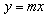 ,把P(4,-2
,把P(4,-2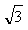 )代入,得
)代入,得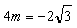
 解得
解得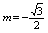 .如果OP∥BD,那么四边形OPBD为平行四边形.
.如果OP∥BD,那么四边形OPBD为平行四边形.
设直线BD的解析式为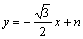 ,将B(6,0)代入,得0=
,将B(6,0)代入,得0=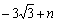 ,所以
,所以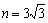
所以直线BD的解析式为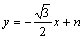 ,
,
解方程组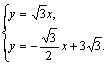 得
得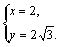
所以D点的坐标为(2,2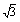 )
)
(3)符合条件的点M存在.验证如下:
过点P作x轴的垂线,垂足为为C,则PC=2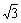 ,AC=2,由勾股定理,可得AP=4,PB=4,又AB=4,所以△APB是等边三角形,只要作∠PA
,AC=2,由勾股定理,可得AP=4,PB=4,又AB=4,所以△APB是等边三角形,只要作∠PA B的平分线交抛物线于M点,连接PM,BM,由于AM=AM, ∠PAM=∠BAM,AB=AP,可得△AMP≌△AMB.因此即存在这样的点M,使△AMP≌△AMB.
B的平分线交抛物线于M点,连接PM,BM,由于AM=AM, ∠PAM=∠BAM,AB=AP,可得△AMP≌△AMB.因此即存在这样的点M,使△AMP≌△AMB.

 阅读快车系列答案
阅读快车系列答案某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整). 已知A、B两组捐款人数的比为1 : 5.
|
|
|


请结合 以上信息解答下列问题.
以上信息解答下列问题.
(1) a= ,本次调查样本的容量是 ;
(2) 先求出C组的人数,再补全“捐款人数分组统计图1”;
(3) 若任意抽出1名学生进行调查,恰好是捐款数不少于30元的概率是多少?
 元二次方程
元二次方程 总有实数根,则
总有实数根,则 应满足的条件是
应满足的条件是 B.
B. C.
C. D.
D.

 米
米 与步行时间
与步行时间 分钟
分钟 所示,则他步行回家的平均速度是 米/分钟.
所示,则他步行回家的平均速度是 米/分钟.
 的两根的平方和是5"则a的值是
的两根的平方和是5"则a的值是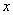 轴,
轴,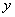 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥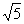 ,反比例函数
,反比例函数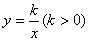 的图象过CD的中点E。
的图象过CD的中点E。 (1)求证:△AOB≌△DCA;
(1)求证:△AOB≌△DCA;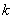 的值;
的值;